Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 7:
a: Xét ΔOAM vuông tại A có
\(\cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AOM}=60^0\)
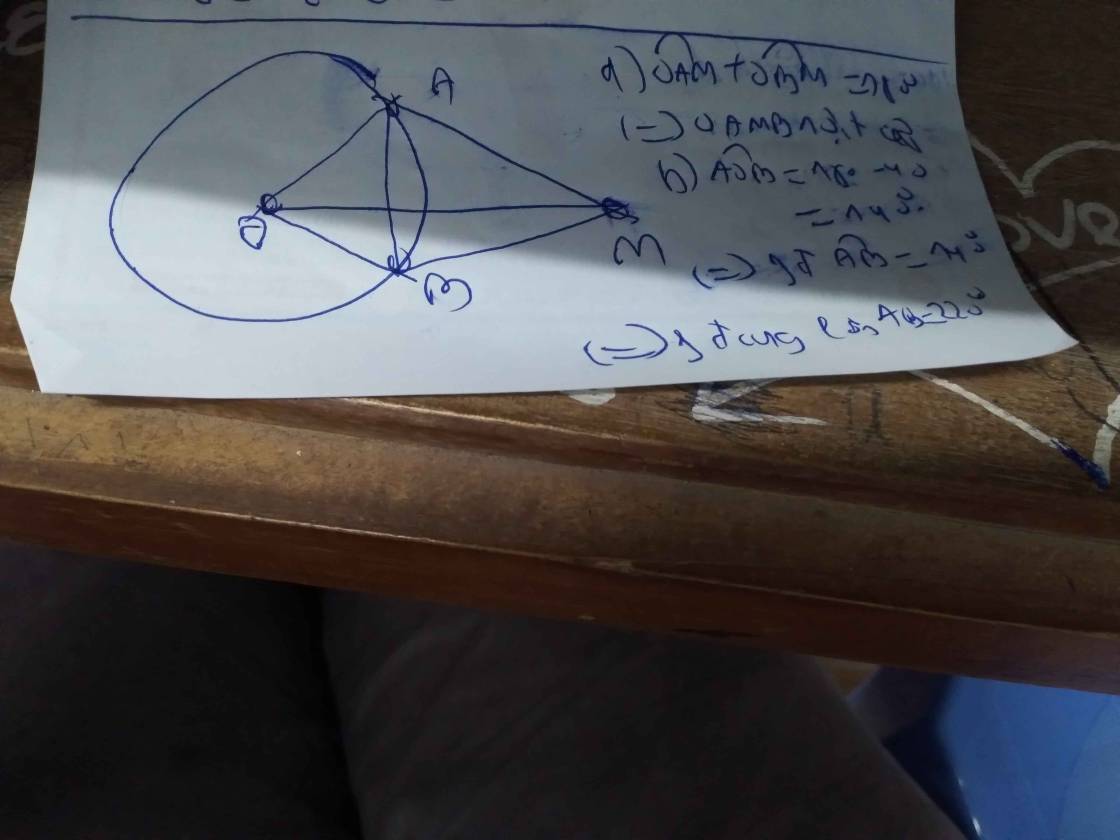
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=180^0\)
Do đó: OAMB là tứ giác nội tiếp
Suy ra: \(\widehat{AOB}=180^0-36^0=144^0\)

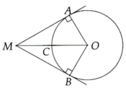
a, Sử dụng tỉ số lượng giác trong tam giác vuông ∆AMO ta tính được A O M ^ = 60 0
b, Tính được A O B ^ = 120 0 , sđ A B C ⏜ = 120 0
c, Ta có A O C ⏜ = B O C ⏜ => A C ⏜ = B C ⏜

O A B M I
Gọi I là trung điêm OM
do đó ta có tính chất của trung tuyến ứng với cạnh huyền lầ
\(IO=IA=IM=\frac{1}{2}OM=\frac{1}{2}.2R=R\)
Xét tam giác IOA có \(IO=OA=AI=R\Rightarrow\)tam giác IOA đều nên IOA = 60 độ
chứng minh tương tự ta sẽ có góc IOB=60 độ
nên AOB=AOI+IOB=120 độ
a: Xét ΔOAM vuông tại A có cosAOM=OA/OM=1/2
nên góc AOM=60 độ
=>sđ cung ANB=gócAOB=2*60=120 độ
b: góc AOB=180-36=144 độ