Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Có \(x+y=2\Rightarrow x^2+2xy+y^2=4\Rightarrow x^2+y^2=4-2.\left(-3\right)=10\)
\(x^4+y^4=\left(x^2\right)^2+\left(y^2\right)^2=\left(x^2+y^2\right)^2-2x^2y^2\)
\(=10^2-2.\left(-3\right)^2=82\)
b. Ta có \(x+y=1\Rightarrow x^2+y^2=1-2xy\)
\(x^3+y^3+3xy=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\)
\(=1.\left(1-2xy-xy\right)+3xy=1\)
Các câu còn lại tương tự

Bài 1.
A = x2 + 2xy + y2 = ( x + y )2 = ( -1 )2 = 1
B = x2 + y2 = ( x2 + 2xy + y2 ) - 2xy = ( x + y )2 - 2xy = (-1)2 - 2.(-12) = 1 + 24 = 25
C = x3 + 3xy( x + y ) + y3 = ( x3 + y3 ) + 3xy( x + y ) = ( x + y )( x2 - xy + y2 ) + 3xy( x + y )
= -1( 25 + 12 ) + 3.(-12).(-1)
= -37 + 36
= -1
D = x3 + y3 = ( x3 + 3x2y + 3xy2 + y3 ) - 3x2y - 3xy2 = ( x + y )3 - 3xy( x + y ) = (-1)3 - 3.(-12).(-1) = -1 - 36 = -37
Bài 2.
M = 3( x2 + y2 ) - 2( x3 + y3 )
= 3( x2 + y2 ) - 2( x + y )( x2 - xy + y2 )
= 3( x2 + y2 ) - 2( x2 - xy + y2 )
= 3x2 + 3y2 - 2x2 + 2xy - 2y2
= x2 + 2xy + y2
= ( x + y )2 = 12 = 1

Bài 1:
a) (x+y)2=92=81
=> x2+2xy+y2=81
=> x2+2.14+y2=81
=> x2+y2=53
=> x2-2xy+y2=81-2.14=25
=> (x-y)2=25
=> x-y=5 hoặc x-y=-5
b) Câu a đã tính được x2+y2=53
c) Ta có: x3+y3=(x+y)(x2-xy+y2)=9(53-14)=9.39=351
Bài 2:
Ta có: \(x^2+2xy+y^2-4x-4y+1=\left(x+y\right)^2-4\left(x+y\right)+1\)
Mà x+y=1
\(\Rightarrow1^2-4.1+1=-2\)
Bài 3:
Ta có: (x+y)3=x3+3x2y+3xy2+y3
= x3+y3+3xy(x+y)
Mà x+y=1 => (x+y)3=x3+y3+3xy=13=1
Bài 4:
Ta có: \(\left(x+y\right)^2=4^2=16\)
\(\Rightarrow x^2+2xy+y^2=16\Rightarrow10+2xy=16\)
\(\Rightarrow2xy=6\Rightarrow xy=3\)
Lại có: \(x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=4.\left(10-3\right)\)
\(=4.7=28\)
Bài 5:
Ta có: \(x^3-y^3-3xy=\left(x-y\right)\left(x^2+xy+y^2\right)-3xy\)
\(=1\left(x^2+xy+y^2\right)-3xy=x^2+xy+y^2-3xy\)
\(=x^2-2xy+y^2=\left(x-y\right)^2=1\)
Mấy bài này đầu hè làm hết rồi:))
Bài 1:
a) \(xy=14\Rightarrow x=\frac{14}{y}\)
Thay vào: \(\frac{14}{y}+y=9\)
\(\Leftrightarrow y^2+14-9y=0\)
\(\Leftrightarrow\left(y-2\right)\left(y-7\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}y=2\\y=7\end{cases}}\Rightarrow\orbr{\begin{cases}x=7\\x=2\end{cases}}\)
+ Nếu: \(\hept{\begin{cases}x=7\\y=2\end{cases}}\Rightarrow x-y=5\)
+ Nếu: \(\hept{\begin{cases}x=2\\y=7\end{cases}}\Rightarrow x-y=-5\)
b) Ta có: \(x+y=9\)
\(\Leftrightarrow\left(x+y\right)^2=81\)
\(\Leftrightarrow x^2+2xy+y^2=81\)
\(\Rightarrow x^2+y^2=81-2xy=81-2.14=53\)
c) Ta có: \(x+y=9\)
\(\Leftrightarrow\left(x+y\right)^3=9^3\)
\(\Leftrightarrow x^3+3x^2y+3xy^2+y^3=729\)
\(\Leftrightarrow x^3+y^3=729-3xy\left(x+y\right)=729-3.14.9=351\)

b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)

\(a)\)\(M=x^3-3xy\left(x-y\right)-y^3-x^2+2xy-y^2\) ( đề nhầm đúng ko bn )
\(M=\left(x^3-3x^2y+3xy^2-y^3\right)-\left(x^2-2xy+y^2\right)\)
\(M=\left(x-y\right)^3-\left(x-y\right)^2\)
\(M=7^3-7^2\)
\(M=294\)
Chúc bạn học tốt ~
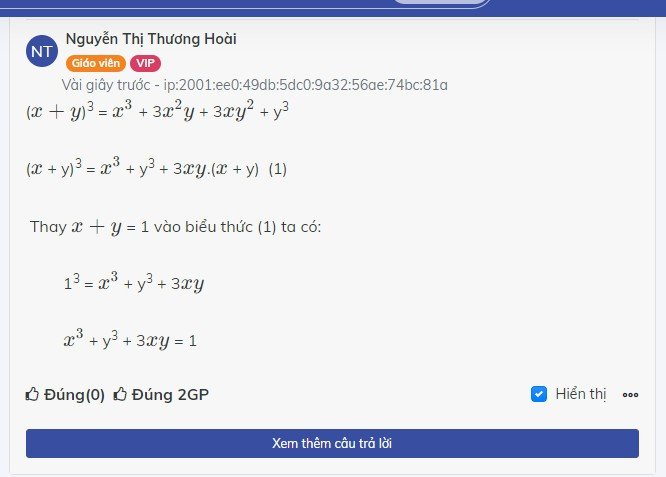
a: \(x^2+y^2=\left(x+y\right)^2-2xy=4-2\cdot\left(-3\right)=10\)
\(x^4+y^4=\left(x^2+y^2\right)^2-2\left(xy\right)^2=100-2\cdot\left(-3\right)^2=100-2\cdot9=82\)
b: \(x^3+y^3+3xy\)
\(=\left(x+y\right)^3-3xy\left(x+y\right)+3xy\)
=1-3xy+3xy=1
d: \(A=\left(x+y\right)^2-4\left(x+y\right)+1=9-4\cdot3+1=10-12=-2\)