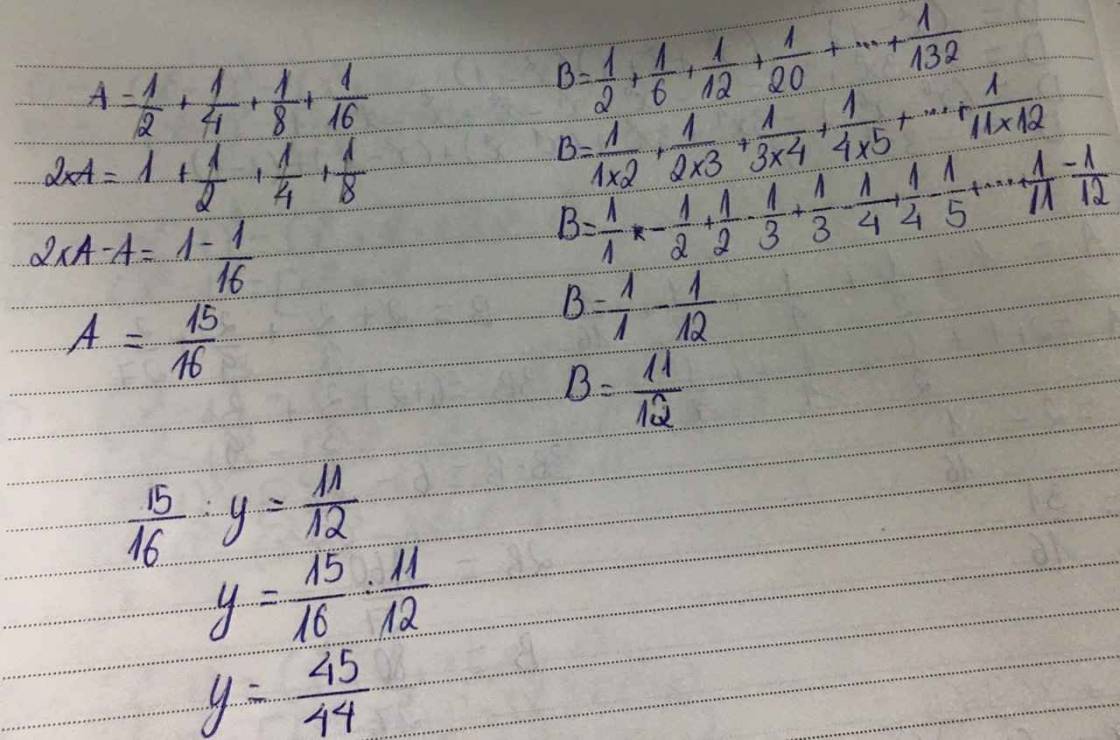Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+..........+\frac{1}{132}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+..........+\frac{1}{11.12}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...........+\frac{1}{11}-\frac{1}{12}\)
\(=1-\frac{1}{12}\)
\(=\frac{11}{12}\)

Ta có : \(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{90}+\frac{1}{110}+\frac{1}{132}\)
= \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}+\frac{1}{10.11}+\frac{1}{11.12}\)
= \(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{9}-\frac{1}{10}+\frac{1}{10}-\frac{1}{11}+\frac{1}{11}-\frac{1}{12}\)
= \(1-\frac{1}{12}=\frac{11}{12}\)

a) A = 2 + 4 + 6 + 8 + ... + 1000
Ta có : A = 2 + 4 + 6 + 8 + ... + 1000 ( có 500 số )
= (1000 + 2) . 500 : 2 = 250500
c) \(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{97.99}+\frac{2}{99.101}\)
\(=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{97}-\frac{1}{99}+\frac{1}{99}-\frac{1}{101}\)
\(=1-\frac{1}{101}=\frac{100}{101}\)

1/2 + 1/6 + 1/12 + ... + 1/132
= 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/11.12
= 1/1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + ... + 1/11 - 1/12
= 1 - 1/12
= 11/12
1/90 + 1/110 + 1/132 + ... + 1/10100
= 1/9.10 + 1/10.11 + 1/11.12 + ... + 1/100.101
= ... [như trên]
= 1/9 - 1/100
= 49/450

2 h 30 chiều nay mình phả đi học rồi , làm ơn giúp mình vói mình xin cảm ơn và sẽ k
\(a,\frac{3}{20}+\frac{3}{20}+\frac{3}{42}+...+\frac{3}{132}\)
\(=3\left(\frac{1}{4\cdot5}+\frac{1}{5\cdot6}+\frac{1}{6\cdot7}+...+\frac{1}{11\cdot12}\right)\)
\(=3\left(\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+...+\frac{1}{11}-\frac{1}{12}\right)\)
\(=3\left(\frac{1}{4}-\frac{1}{12}\right)\)
\(=3\cdot\frac{1}{6}=\frac{1}{2}\)

1/12 + 1/20 + ... + 1/132
= 1/3×4 + 1/4×5 + ... + 1/11×12
= 1/3 - 1/4 + 1/4 - 1/5 + ... + 1/11 - 1/12
= 1/3 - 1/12
= 4/12 - 1/12
= 3/12 = 1/4

\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{110}+\frac{1}{132}\)
= \(\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+\frac{1}{4\times5}+...+\frac{1}{10\times11}+\frac{1}{11\times12}\)
= \(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{10}-\frac{1}{11}+\frac{1}{11}-\frac{1}{12}\)
= \(\frac{1}{1}-\frac{1}{12}\)
= \(\frac{11}{12}\)
Ta có : \(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+......+\frac{1}{132}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+......+\frac{1}{11.12}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+......+\frac{1}{11}-\frac{1}{12}\)
\(=1-\frac{1}{12}\)
\(=\frac{11}{12}\)