Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Ta có 
= 22 +2.2 +4 = 12.
Vì 
nên hàm số y = g(x) gián đoạn tại x0 = 2.
b) Để hàm số y = f(x) liên tục tại x0 = 2 thì ta cần thay số 5 bởi số 12
a) Các bạn tự vẽ hình nhé . Đồ thị hàm số y = f(x) là một đường không liền nét mà bị đứt quãng tại x0 = -1. Vậy hàm số đã cho liên tục trên khoảng (-∞; -1) và (- 1; +∞).
b) +) Nếu x < -1: f(x) = 3x + 2 liên tục trên (-∞; -1) (vì đây là hàm đa thức).
+) Nếu x> -1: f(x) = x2 – 1 liên tục trên (-1; +∞) (vì đây là hàm đa thức).
+) Tại x = -1;
Ta có =
= 3(-1) +2 = -1.
= (-1)2 – 1 = 0.
Vì 
nên không tồn tại 
. Vậy hàm số gián đoạn tại
x0 = -1.
TenAnh1 TenAnh1 A = (-0.04, -7.12) A = (-0.04, -7.12) A = (-0.04, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) D = (10.58, -5.6) D = (10.58, -5.6) D = (10.58, -5.6)
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\frac{\sqrt{3x+1}-2}{x-1}=\lim\limits_{x\rightarrow1}\frac{\left(\sqrt{3x+1}-2\right)\left(\sqrt{3x+1}+2\right)}{\left(x-1\right)\left(\sqrt{3x+1}+2\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{3\left(x-1\right)}{\left(x-1\right)\left(\sqrt{3x+1}+2\right)}=\lim\limits_{x\rightarrow1}\frac{3}{\sqrt{3x+1}+2}=\frac{3}{4}\)
\(\Rightarrow\) Để hàm số liên tục tại x=1
\(\Leftrightarrow f\left(1\right)=\lim\limits_{x\rightarrow1}f\left(x\right)\Leftrightarrow m=\frac{3}{4}\)
Ta có:
limx→2+g(x)=limx→2+x2−x−2x−2=limx→2+(x−2)(x+1)x−2=limx→2+(x+1)=3limx→2+g(x)=limx→2+x2−x−2x−2=limx→2+(x−2)(x+1)x−2=limx→2+(x+1)=3
(1)
limx→2−g(x)=limx→2−(5−x)=3limx→2−g(x)=limx→2−(5−x)=3(2)
g(2) = 5 – 2 = 3 (3)
Từ (1), (2) và (3) suy ra: limx→2g(x)=g(2)limx→2g(x)=g(2) .
Do đó hàm số y = g(x) liên tục tại x0 = 2
_ Mặt khác trên (-∞, 2), g(x) là hàm đa thức và trên (2, +∞), g(x) là hàm số phân thức hữu tỉ xác định trên (2, +∞) nên hàm số g(x) liên tục trên hai khoảng (-∞, 2) và (2, +∞)
Vậy hàm số y = g(x) liêu tục trên R.
TenAnh1 TenAnh1 A = (-0.04, -7.12) A = (-0.04, -7.12) A = (-0.04, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) B = (15.32, -7.12) C = (-4.78, -5.6) C = (-4.78, -5.6) C = (-4.78, -5.6) D = (7.82, -7.32) D = (7.82, -7.32) D = (7.82, -7.32) E = (-4.82, -6.92) E = (-4.82, -6.92) E = (-4.82, -6.92) F = (10.54, -6.92) F = (10.54, -6.92) F = (10.54, -6.92) G = (-7.14, -8.07) G = (-7.14, -8.07) G = (-7.14, -8.07) H = (12.33, -8.07) H = (12.33, -8.07) H = (12.33, -8.07)
\(\lim\limits_{x\rightarrow0}\left|f\left(x\right)\right|=\lim\limits_{x\rightarrow0}\left|x^2sin\dfrac{1}{x}\right|< \lim\limits_{x\rightarrow0}\left|x^2\right|=0\).
Vậy \(\lim\limits_{x\rightarrow0}f\left(x\right)=0\).
\(f\left(0\right)=A\).
Để hàm số liên tục tại \(x=0\) thì \(\lim\limits_{x\rightarrow0}f\left(x\right)=f\left(0\right)\Leftrightarrow A=0\).
Để xét hàm số có đạo hàm tại \(x=0\) ta xét giới hạn:
\(\lim\limits_{x\rightarrow0}\dfrac{f\left(x\right)-f\left(0\right)}{x-0}=\lim\limits_{x\rightarrow0}\dfrac{x^2sin\dfrac{1}{x}}{x}=\lim\limits_{x\rightarrow0}xsin\dfrac{1}{x}=0\).
Vậy hàm số có đạo hàm tại \(x=0\).
a) Ta có g(x) =
=
(x2 + 2x + 4) = 22 +2.2 +4 = 12.
Vì g(x) ≠ g(2) nên hàm số y = g(x) gián đoạn tại x0 = 2.
b) Để hàm số y = f(x) liên tục tại x0 = 2 thì ta cần thay số 5 bởi số 12.
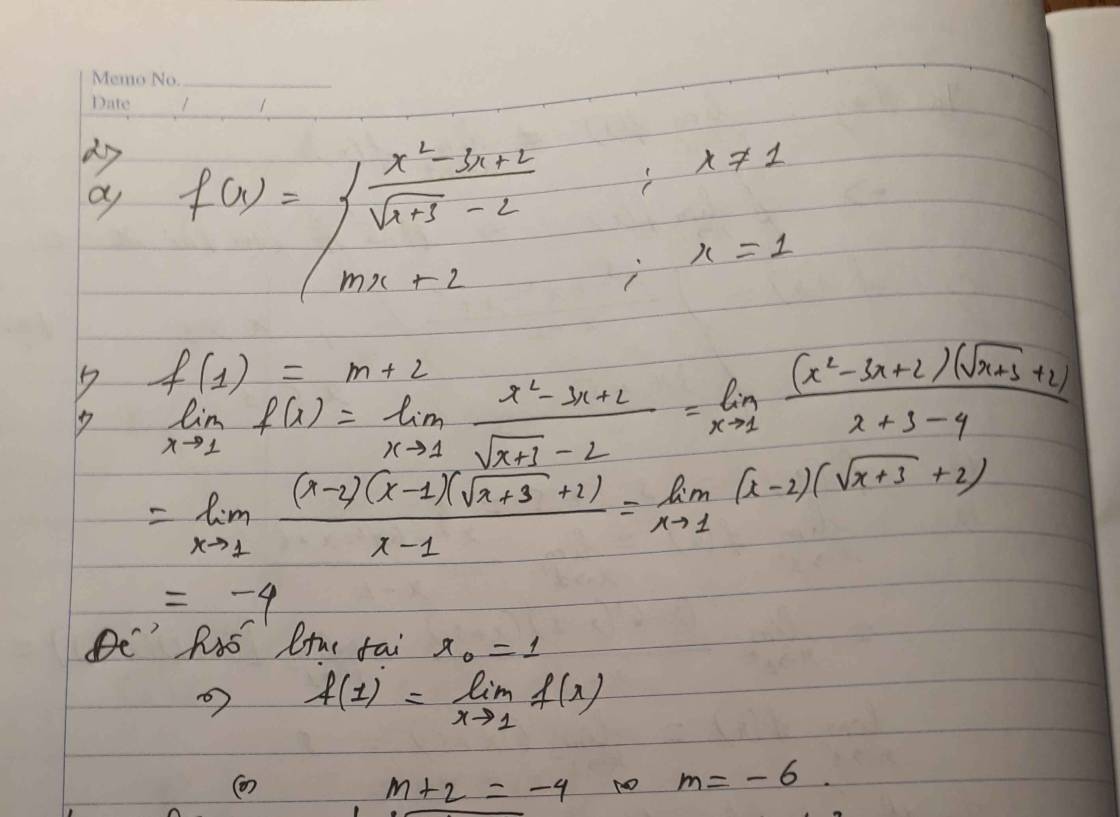
\(\lim\limits_{x\rightarrow2}g\left(x\right)=\lim\limits_{x\rightarrow2}\frac{x^3-8}{x-1}=\frac{0}{1}=0\)
\(g\left(2\right)=5\)
\(\Rightarrow\lim\limits_{x\rightarrow2}g\left(x\right)\ne g\left(2\right)\Rightarrow g\left(x\right)\) ko liên tục tại x=2
b/ Ko thấy số 5 nào ở biểu thức g(x) cả