Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$(P):y=x^2+bx+2$ đi qua $(3;-4)$ nên:
$-4=3^2+b.3+2\Rightarrow b=-5$
Vậy pt cần tìm là $y=x^2-5x+2$
Vậy thì trục đối xứng $x=\frac{-3}{2}$ có vẻ thừa?

Lời giải
a)
a.1) Trục đối xứng y =1/4
a.2) giao trục tung A(0,-2)
a.3) giao trục hoành (\(\left(\Delta=17\right)\) \(B\left(\dfrac{1-\sqrt{17}}{4};0\right)\);\(C\left(\dfrac{1+\sqrt{17}}{4}\right)\)
b)
b.1) Trục đối xứng y =-1/4
b.2) giao trục tung A(0,2)
a.3) giao trục hoành \(\left(\Delta=17\right)\) \(B\left(\dfrac{-1-\sqrt{17}}{4};0\right)\);\(C\left(\dfrac{-1+\sqrt{17}}{4}\right)\)

Do đồ thị (P) có trục đối xứng \(x=1\Rightarrow\frac{-b}{2.2}=1\Rightarrow b=-4\)
\(\Rightarrow y=2x^2-4x+c\)
Do (P) qua \(M\left(0;4\right)\Rightarrow2.0-4.0+c=4\Rightarrow c=4\)
Phương trình (P): \(y=2x^2-4x+4\)

a) Vì parabol đi qua M(1; 5) nên tọa độ của M nghiệm đúng phương trình của parabol: 5 = a.12 + b.1 + 2.
Tương tự, với N(- 2; 8) ta có: 8 = a.(- 2)2 + b.(- 2) + 2
Giải hệ phương trình: ta được a = 2, b = 1.
Parabol có phương trình là: y = 2x2 + x + 2.
b) Giải hệ phương trình:
Parabol: y = x2 - x + 2.
c) Giải hệ phương trình:
Parabol: y = x2 - 4x + 2.
d) Ta có:
Parabol: y = 16x2 + 12x + 2 hoặc y = x2 - 3x + 2.

\(\left(P\right):y=ax^2+bx+2\)
Vì (P) đi qua điểm \(M\left(1;5\right)\) nên ta có: \(a.1^2+b.1+2=5\Leftrightarrow a+b=3\) (1)
Mà (P) có trục đối xứng là \(x=\dfrac{-1}{4}\) nên: \(\dfrac{-b}{2a}=\dfrac{-1}{4}\)
\(\Leftrightarrow-2a=-4b\Leftrightarrow-2a+4b=0\) (2)
Từ (1) và (2) ta có:
\(\left\{{}\begin{matrix}a+b=3\\-2a+4b=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=1\end{matrix}\right.\)
Vậy parabol cần tìm có dạng: \(y=2x^2=x+2\)
xác định parabol (p): y= ax^2+2x+c biết rằng i (1/2; 11/2) là đỉnh của (p)
giải dùm t câu này vs c
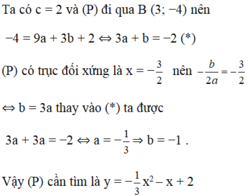

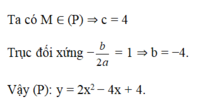
Đề sai rồi bạn
Trục đối xứng là 2
=> -b/2a = 2
=> a = -b/4 = - (-4)/4 = 1
P đi qua A(1;2)
=> 2 = 1.1^2 - 4.1 + c
=> c + 1 - 4 = 2
=> c = 5
=> y = x^2 - 4x + 5