Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo:
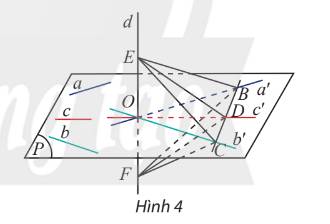
a) Vì a//a', d⊥a nên d⊥a′, Hay EF⊥OB
Tam giác EBF có OB⊥EF; O là trung điểm EF nên tam giác EBF cân tại B. Suy ra BE = BF
Tương tự ta chứng minh được CE = CF
Suy ra tam giác CEB bằng tam giác CFB
b) Vì tam giác CEB và CFB bằng nhau nên DE = DF
Nên tam giác DEF cân tại D có DO là trung tuyến nên DO⊥EF
Suy ra d⊥c

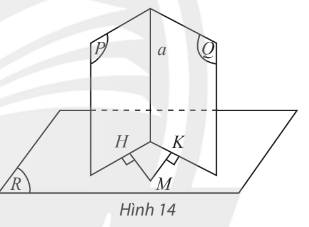
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}M \in \left( R \right)\\MH \bot \left( P \right)\\\left( R \right) \bot \left( P \right)\end{array} \right\} \Rightarrow MH \subset \left( R \right)\\\left. \begin{array}{l}M \in \left( R \right)\\MK \bot \left( Q \right)\\\left( R \right) \bot \left( Q \right)\end{array} \right\} \Rightarrow MK \subset \left( R \right)\end{array}\)
b) Ta có:
\(\left. \begin{array}{l}MH \bot \left( P \right) \Rightarrow MH \bot a\\MK \bot \left( Q \right) \Rightarrow MK \bot a\\MH,MK \subset \left( R \right)\end{array} \right\} \Rightarrow a \bot \left( R \right)\)

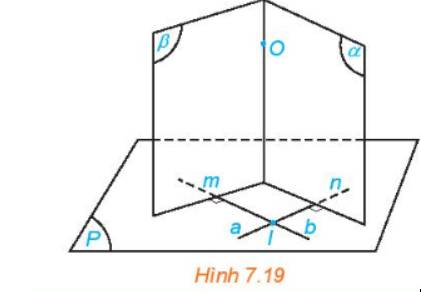
a) Vì \(\left( \alpha \right),\left( \beta \right)\) là các mặt phẳng qua O và giao 2 mặt phẳng là 1 đường thẳng nên hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) cắt nhau theo một đường thẳng đi qua O.
b) Gọi \(\Delta \) là giao tuyến của 2 \(\left( \alpha \right),\left( \beta \right)\)
\(\left. \begin{array}{l}a \bot \left( \alpha \right)\\\Delta \subset \left( \alpha \right)\end{array} \right\} \Rightarrow a \bot \Delta \)
\(\left. \begin{array}{l}b \bot \left( \beta \right)\\\Delta \subset \left( \beta \right)\end{array} \right\} \Rightarrow b \bot \Delta \)
Mà \(a \cap b = \left\{ I \right\} \Rightarrow \Delta \bot \left( P \right)\)

a) Qua điểm \(A\), ta vẽ được duy nhất một đường thẳng \(a\) song song với đường thẳng \(a'\).
Qua điểm \(A\), ta vẽ được duy nhất một đường thẳng \(b\) song song với đường thẳng \(b'\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}a\parallel a'\\a' \subset \left( Q \right)\end{array} \right\} \Rightarrow a\parallel \left( Q \right)\\\left. \begin{array}{l}b\parallel b'\\b' \subset \left( Q \right)\end{array} \right\} \Rightarrow b\parallel \left( Q \right)\end{array}\)
b) Ta có:
\(\left. \begin{array}{l}a\parallel \left( Q \right)\\b\parallel \left( Q \right)\\a,b \subset mp\left( {a,b} \right)\end{array} \right\} \Rightarrow mp\left( {a,b} \right)\parallel \left( Q \right)\)

Áp dụng tính chất 2, ta có \(\left( P \right)\) là mặt phẳng duy nhất đi qua ba điểm phân biệt \(A,B,C\) là mặt phẳng \(M,N,O\).
Áp dụng tính chất 3, ta có
– Đường thẳng \(a\) có hai điểm phân biệt \(M,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(a\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(a\) nằm trong mặt phẳng \(\left( P \right)\).
– Đường thẳng \(b\) có hai điểm phân biệt \(N,O\) nằm trong mặt phẳng \(\left( P \right)\) nên mọi điểm của đường thẳng \(b\) cũng nằm trong mặt phẳng \(\left( P \right)\). Vậy đường thẳng \(b\) nằm trong mặt phẳng \(\left( P \right)\).

Gọi (R) là mặt phẳng chứa a và (R)//(Q)
(Q)//(R)
\(\left(P\right)\cap\left(Q\right)=a'\)
\(\left(P\right)\cap\left(R\right)=a\)
Do đó: a//a'
mà IJ vuông góc a
nên JI vuông góc a'
\(\left(P\right)\perp\left(Q\right)\)
\(\left(P\right)\cap\left(Q\right)=a'\)
\(JI\perp a\)
Do đó: JI vuông góc (Q)
=>IJ vuông góc b
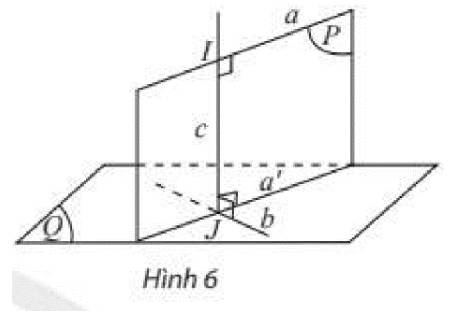
tham khảo:
Gọi (R) là mặt phẳng chứa a song song với (Q).
(P) cắt hai mặt phẳng song song tại a và a' nên a//a'
Trong mặt phẳng (P), IJ⊥a,a//a′ nên IJ⊥a′
Ta có: (P)⊥(Q), (P) cắt (Q) tại a', IJ⊥a′ nên IJ⊥(P)
Suy ra IJ⊥b

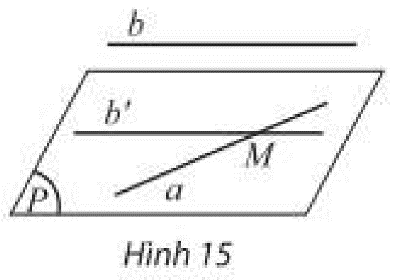
a) Ta có:
\(\left. \begin{array}{l}b\parallel b'\\b' \subset \left( P \right)\end{array} \right\} \Rightarrow b\parallel \left( P \right)\)
b) Theo hệ quả 1, ta có:
\(\left. \begin{array}{l}b\parallel \left( {P'} \right)\\M \in b'\\b\parallel b'\end{array} \right\} \Rightarrow b' \subset \left( {P'} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}a \subset \left( P \right)\\a \subset \left( {P'} \right)\end{array} \right\} \Rightarrow a = \left( P \right) \cap \left( {P'} \right)\\\left. \begin{array}{l}b' \subset \left( P \right)\\b' \subset \left( {P'} \right)\end{array} \right\} \Rightarrow b' = \left( P \right) \cap \left( {P'} \right)\end{array}\)
Do đó \(a\) và \(b'\) đều là các đường thẳng chung của hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\).
Vì \(a\) và \(b'\) phân biệt, mà hai mặt phẳng phân biệt chỉ có duy nhất một đường thẳng chung nên \(\left( P \right) \equiv \left( {P'} \right)\).

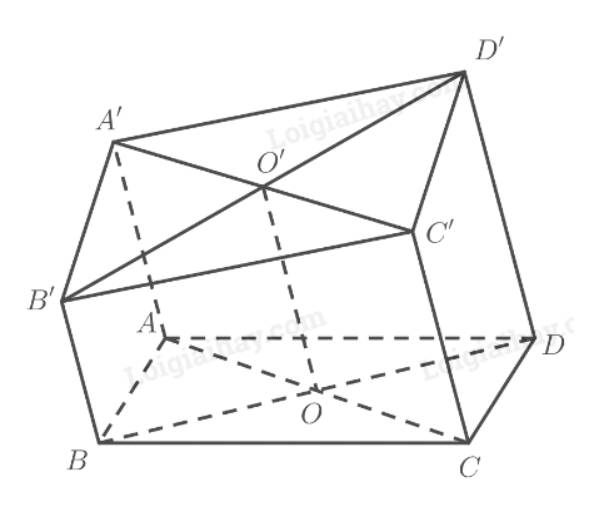
a) Ta có:
\(\left. \begin{array}{l}AA'\parallel DD'\\DD' \subset \left( {CC'D'D} \right)\end{array} \right\} \Rightarrow AA'\parallel \left( {CC'D'D} \right)\)
\(\left. \begin{array}{l}AB\parallel C{\rm{D}}\\C{\rm{D}} \subset \left( {CC'D'D} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {CC'D'D} \right)\)
\(\left. \begin{array}{l}AA'\parallel \left( {CC'D'D} \right)\\AB\parallel \left( {CC'D'D} \right)\\AA',AB \subset \left( {AA'B'B} \right)\end{array} \right\} \Rightarrow \left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( P \right) \cap \left( {AA'B'B} \right) = A'B'\\\left( P \right) \cap \left( {CC'D'D} \right) = C'D'\end{array} \right\} \Rightarrow A'B'\parallel C'D'\left( 1 \right)\)
\(\left. \begin{array}{l}AD\parallel BC\\BC \subset \left( {BB'C'C} \right)\end{array} \right\} \Rightarrow AD\parallel \left( {BB'C'C} \right)\)
\(\left. \begin{array}{l}AA'\parallel BB'\\BB' \subset \left( {BB'C'C} \right)\end{array} \right\} \Rightarrow AA'\parallel \left( {BB'C'C} \right)\)
\(\left. \begin{array}{l}AA'\parallel \left( {BB'C'C} \right)\\AD\parallel \left( {BB'C'C} \right)\\AA',AD \subset \left( {AA'D'D} \right)\end{array} \right\} \Rightarrow \left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\)
\(\left. \begin{array}{l}\left( {AA'D'D} \right)\parallel \left( {BB'C'C} \right)\\\left( P \right) \cap \left( {AA'D'D} \right) = A'D'\\\left( P \right) \cap \left( {BB'C'C} \right) = B'C'\end{array} \right\} \Rightarrow A'D'\parallel B'C'\left( 2 \right)\)
Từ (1) và (2) suy ra \(A'B'C'D'\) là hình bình hành.
Gọi \(O = AC \cap B{\rm{D}},O' = A'C' \cap B'{\rm{D}}'\)
\( \Rightarrow O\) là trung điểm của \(AC,B{\rm{D}}\), \(O'\) là trung điểm của \(A'C',B'{\rm{D}}'\).
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( {AA'C'C} \right) \cap \left( {AA'B'B} \right) = AA'\\\left( {AA'C'C} \right) \cap \left( {CC'D'D} \right) = CC'\end{array} \right\} \Rightarrow AA'\parallel CC'\)
\( \Rightarrow AA'C'C\) là hình thang
\(O\) là trung điểm của \(AC\)
\(O'\) là trung điểm của \(A'C'\)
\( \Rightarrow OO'\) là đường trung bình của hình thang \(AA'C'C\)
\( \Rightarrow AA' + CC' = 2OO'\left( 3 \right)\)
\(\left. \begin{array}{l}\left( {AA'B'B} \right)\parallel \left( {CC'D'D} \right)\\\left( {BB'D'D} \right) \cap \left( {AA'B'B} \right) = BB'\\\left( {BB'D'D} \right) \cap \left( {CC'D'D} \right) = DD'\end{array} \right\} \Rightarrow BB'\parallel DD'\)
\( \Rightarrow BB'D'D\) là hình thang
\(O\) là trung điểm của \(B{\rm{D}}\)
\(O'\) là trung điểm của \(B'D'\)
\( \Rightarrow OO'\) là đường trung bình của hình thang \(BB'D'D\)
\( \Rightarrow BB' + DD' = 2OO'\left( 4 \right)\)
Từ (3) và (4) suy ra \(AA' + CC' = BB' + DD'\left( { = 2OO'} \right)\).

tham khảo:
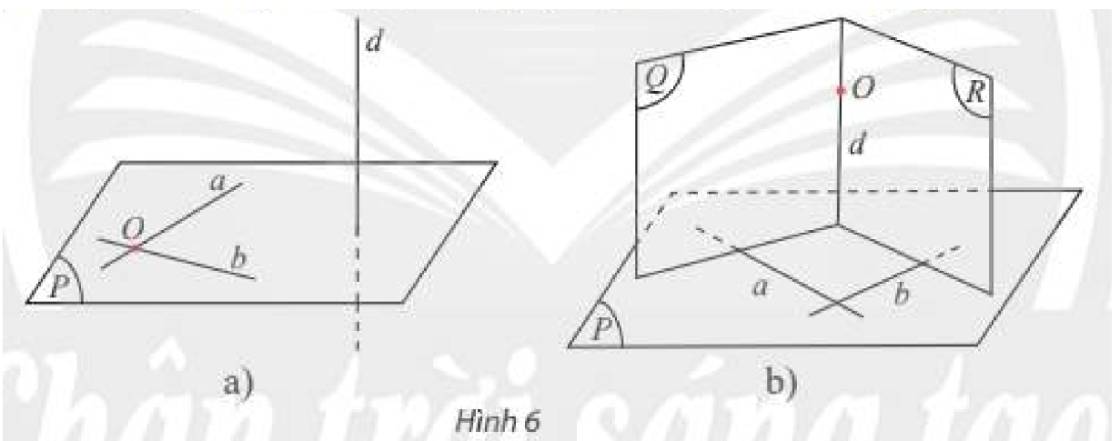
a) Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)
b) Vì a⊥(Q);d∈(Q) nên a⊥d
Vì b⊥(R),d∈(R) nên b⊥d
Vì đường thẳng d vuông góc hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng (P) nên d⊥(P)