Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(\left\{ \begin{array}{l}JC \bot AE\\BH \bot AE\end{array} \right. \Rightarrow JC//BH\). Vì \(JC//BH \Rightarrow \widehat {HBA} = \widehat {JCA}\) (hai góc đồng vị)
hay \(\widehat {HBA} = \widehat {DCB}\)
Xét \(\Delta ABH\) và \(\Delta DCB\) có:
\(\widehat {HBA} = \widehat {DCB}\) (chứng minh trên)
\(\widehat {AHB} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta ABH\backsim\Delta DCB\) (g.g)
b) Vì (hai góc tương ứng) hay \(\widehat {EAB} = \widehat {CDB}\).
Xét \(\Delta AEB\) và \(\Delta DCB\) có:
\(\widehat {EAB} = \widehat {CDB}\) (chứng minh trên)
\(\widehat {ABE} = \widehat {DBC} = 90^\circ \)
Do đó, \(\Delta AEB\backsim\Delta DCB\) (g.g)
Suy ra, \(\frac{{BE}}{{BC}} = \frac{{BA}}{{BD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Hay \(\frac{{BC}}{{BE}} = \frac{{BD}}{{BA}}\) (điều phải chứng minh).

a) Xét tam giác \(ABD\) và tam giác \(ACB\) có:
\(\widehat {ABD} = \widehat {ACB}\) (giả thuyết)
\(\widehat A\) chung
Suy ra, \(\Delta ABD\backsim\Delta ACB\) (g.g)
b) Vì \(\Delta ABD\backsim\Delta ACB\)
Suy ra, \(\frac{{AB}}{{AC}} = \frac{{AD}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Suy ra, \(A{B^2} = AC.AD = 9.4 = 36 \Rightarrow AB = \sqrt {36} = 6\)
Vậy \(AB = 6cm.\)

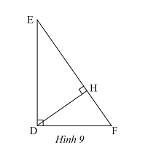
a) Xét \(\Delta DEF\) và \(\Delta HDF\) có:
\(\widehat F\) chung
\(\widehat {EDF} = \widehat {DHF} = 90^\circ \)
Do đó, \(\Delta DEF\backsim\Delta HDF\) (g.g)
b) Vì \(\Delta DEF\backsim\Delta HDF\) nên \(\frac{{DF}}{{HF}} = \frac{{FE}}{{DF}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
\( \Rightarrow D{F^2} = FH.FE\).
c) Theo câu b ta có:
\(D{F^2} = FH.FE\)
Thay số, \(D{F^2} = 5,4.15 = 81 \Rightarrow DF = \sqrt {81} = 9cm\)
Vậy \(DF = 9cm\).

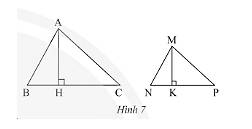
a) Vì tam giác \(\Delta MNP\backsim\Delta ABC\) nên \(\widehat B = \widehat N\) (hai góc tương ứng).
Vì \(MK\) là đường cao nên \(\widehat {MKN} = 90^\circ \);Vì \(AH\) là đường cao nên \(\widehat {AHB} = 90^\circ \)
Xét \(\Delta MNK\) và \(\Delta ABH\) có:
\(\widehat B = \widehat N\) (chứng minh trên)
\(\widehat {MKN} = \widehat {AHB} = 90^\circ \)
Do đó, \(\Delta MNK\backsim\Delta ABH\) (g.g)
Vì \(\Delta MNK\backsim\Delta ABH\) nên ta có: \(\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k\).
b) Vì \(\Delta MNP\backsim\Delta ABC\) nên \(\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k\)
\( \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC\)
Vì \(\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH\)
Diện tích tam giác \(MNP\) là:
\({S_1} = \frac{1}{2}.MK.NP\) (đvdt)
Diện tích tam giác \(ABC\) là:
\({S_2} = \frac{1}{2}.AH.BC\) (đvdt)
Ta có: \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}\) (điều phải chứng minh)

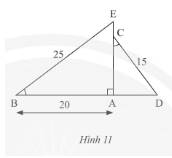
Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(\widehat {EBA} = \widehat {ACD}\) (giả thuyết)
\(\widehat {BAE} = \widehat {CAD} = 90^\circ \)
Do đó, \(\Delta ABE\backsim\Delta ACD\) (g.g)
Vì \(\Delta ABE\backsim\Delta ACD\) nên \(\frac{{AB}}{{AC}} = \frac{{EB}}{{CD}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{20}}{{AC}} = \frac{{25}}{{15}} \Rightarrow AC = \frac{{20.15}}{{25}} = 12\)cm.
Áp dụng định lí Py – ta – go cho \(\Delta ABE\) vuông tại \(A\) ta có:
\(B{E^2} = A{E^2} + A{B^2} \Leftrightarrow A{E^2} = B{E^2} - A{B^2} = {25^2} - {20^2} = 225 \Rightarrow AE = \sqrt {225} = 15\)cm.
Độ dài \(CE\) là:
15 – 12 = 3cm
Vậy \(CE = 3cm.\)

Tỉ số:
\(\frac{{DE}}{{AC}} = \frac{6}{8} = \frac{3}{4};\frac{{EF}}{{BC}} = \frac{{15}}{{20}} = \frac{3}{4}\).
Xét tam giác\(DEF\) và tam giác\(ABC\) có:
\(\frac{{DE}}{{AC}} = \frac{{EF}}{{BC}} = \frac{3}{4}\) (chứng minh trên)
Do đó, \(\Delta DEF\backsim\Delta ABC\).
Tỉ số:
\(\frac{{DE}}{{MN}} = \frac{6}{3} = 2;\frac{{EF}}{{NP}} = \frac{{15}}{6} = \frac{5}{2}\).
Vì \(\frac{{DE}}{{MN}} \ne \frac{{EF}}{{NP}}\) nên hai tam giác \(DEF\) và \(MNP\) không đồng dạng với nhau.
Tỉ số:
\(\frac{{DE}}{{RS}} = \frac{6}{4} = \frac{3}{2};\frac{{EF}}{{ST}} = \frac{{15}}{{12}} = \frac{5}{4}\).
Vì \(\frac{{DE}}{{RS}} \ne \frac{{EF}}{{ST}}\) nên hai tam giác \(DEF\) và \(SRT\) không đồng dạng với nhau.

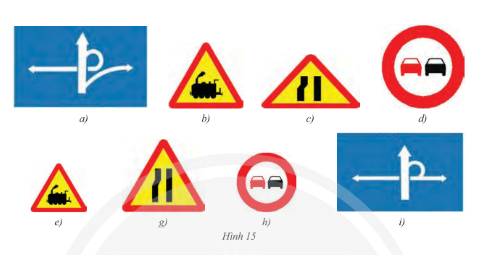
Các cặp hình đồng dạng là:
- Hình a và hình i đồng dạng với nhau;
- Hình b và hình e đồng dạng với nhau;
- Hình c và hình g đồng dạng với nhau;
- Hình d và hình h đồng dạng với nhau.

Xét tam giác vuông \(PQR\) có:
\(\widehat P + \widehat Q + \widehat R = 180^\circ \Leftrightarrow \widehat P + 90^\circ + 42^\circ = 180^\circ \Rightarrow \widehat P = 180^\circ - 90^\circ - 42^\circ = 48^\circ \)
Xét tam giác vuông \(UVT\) có:
\(U{V^2} = U{T^2} + V{T^2} \Leftrightarrow {6^2} = U{T^2} + {4^2} \Rightarrow U{T^2} = {6^2} - {4^2} = 20 \Rightarrow UT = 2\sqrt 5 \)
Xét tam giác vuông \(DEF\) có:
\(E{F^2} = D{E^2} + D{F^2} \Leftrightarrow E{F^2} = {9^2} + {12^2} \Rightarrow E{F^2} = 225 \Rightarrow EF = 15\)
Xét tam giác vuông \(MNK\) có:
\(K{N^2} = K{M^2} + M{N^2} \Leftrightarrow {9^2} = K{M^2} + {6^2} \Rightarrow K{M^2} = {9^2} - {6^2} = 45 \Rightarrow KM = 3\sqrt 5 \)
Xét tam giác vuông \(IGH\) có:
\(I{H^2} = H{G^2} + I{G^2} \Leftrightarrow I{H^2} = 7,{5^2} + {10^2} \Rightarrow I{H^2} = 156,25 \Rightarrow IH = 12,5\)
- Xét \(\Delta ABC\) và \(\Delta QPR\) có:
\(\widehat B = \widehat P = 48^\circ \) (chứng minh trên)
\(\widehat A = \widehat Q = 90^\circ \)
Do đó, \(\Delta ABC\backsim\Delta QPR\) (g.g)
- Xét \(\Delta UTV\) và \(\Delta KMN\) có:
\(\widehat T = \widehat M = 90^\circ \)
\(\frac{{UT}}{{KM}} = \frac{{2\sqrt 5 }}{{3\sqrt 5 }} = \frac{2}{3};\frac{{VT}}{{MN}} = \frac{4}{6} = \frac{2}{3}\)
Do đó, \(\Delta UTV\backsim\Delta KMN\) (c.g.c)
- Xét \(\Delta DEF\) và \(\Delta GHI\) có:
\(\widehat D = \widehat G = 90^\circ \)
\(\frac{{HG}}{{DE}} = \frac{{7,5}}{9} = \frac{5}{6};\frac{{IG}}{{DF}} = \frac{{10}}{{12}} = \frac{5}{6}\)
Do đó, \(\Delta DEF\backsim\Delta GHI\) (c.g.c).

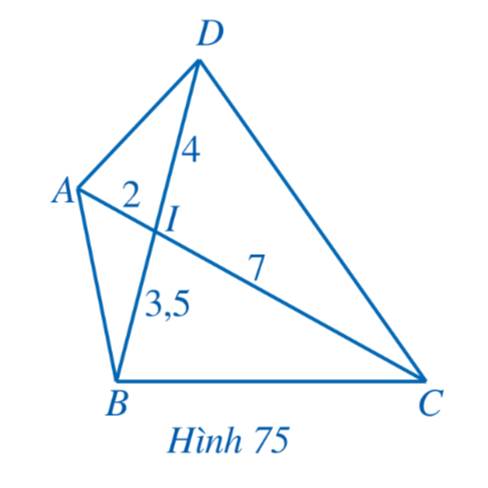
a) Ta thấy \(\frac{{IA}}{{ID}} = \frac{2}{4} = \frac{1}{2};\,\,\frac{{IB}}{{IC}} = \frac{3}{6} = \frac{1}{2}\)
\( \Rightarrow \frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\)
Mà \(\widehat {AIB} = \widehat {DIC}\) (hai góc đối đỉnh)
Xét tam giác IAB và tam giác IDC có:
\(\frac{{IA}}{{ID}} = \frac{{IB}}{{IC}}\) và \(\widehat {AIB} = \widehat {DIC}\)
\( \Rightarrow \)\(\Delta IAB \backsim \Delta IDC\) (c-g-c)
b) Ta thấy \(\frac{{IA}}{{IB}} = \frac{2}{3};\,\,\frac{{ID}}{{IC}} = \frac{4}{6} = \frac{2}{3}\)
\( \Rightarrow \frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\)
Mà \(\widehat {AID} = \widehat {BIC}\) (hai góc đối đỉnh)
Xét tam giác IAD và tam giác IBC có:
\(\frac{{IA}}{{IB}} = \frac{{ID}}{{IC}}\) và \(\widehat {AID} = \widehat {BIC}\)
\( \Rightarrow \)\(\Delta IAD \backsim \Delta IBC\) (c-g-c)





a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
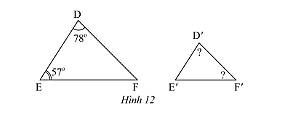
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
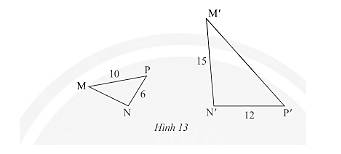
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).