Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(S = \frac{{{u_1}}}{{1 - q}} = \frac{{\frac{2}{3}}}{{1 - \frac{{ - 1}}{4}}} = \frac{8}{{15}}\)
b) \(1,\left( 6 \right) = \frac{5}{3}\)

\(a=34,\left(12\right)\)
\(=34\dfrac{12}{99}=34\dfrac{4}{33}=\dfrac{1126}{33}\)

Đáp án B
- Cách giải:
Cho cấp số nhân lùi vô hạn
u
n
có công bội q. Khi đó tổng của cấp số nhân lùi vô hạn đó được tính bởi công thức 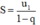

1. Bạn ghi lại đề, mẫu số ko rõ
2. \(=lim\left[-8n^6\left(1-\frac{4}{n^2}\right)^3\right]=-\infty.1=-\infty\)
3. Dãy số là CSC với \(\left\{{}\begin{matrix}u_1=-1\\d=3\end{matrix}\right.\) \(\Rightarrow u_n=-1+\left(n-1\right)3=3n-4\)
\(\Rightarrow lim\frac{3n-4}{5n+2020}=lim\frac{3-\frac{4}{n}}{5+\frac{2020}{n}}=\frac{3}{5}\)
4.
\(u_{n+1}=\frac{1}{2}u_n+\frac{3}{2}\Rightarrow u_{n+1}-3=\frac{1}{2}\left(u_n-3\right)\)
Đặt \(v_n=u_n-3\Rightarrow\left\{{}\begin{matrix}v_1=-2\\v_{n+1}=\frac{1}{2}v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội \(\frac{1}{2}\Rightarrow v_n=-2.\frac{1}{2^{n-1}}\Rightarrow u_n=v_n+3=-\frac{1}{2^{n-2}}+3\)
\(\Rightarrow lim\left(u_n\right)=lim\left[-\frac{1}{2^{n-2}}+3\right]=3\)
5.
\(u_{n+1}=u_n+\frac{1}{2^n}\Rightarrow u_{n+1}+\frac{2}{2^{n+1}}=u_n+\frac{2}{2^n}\)
Đặt \(v_n=u_n+\frac{2}{2^n}\Rightarrow\left\{{}\begin{matrix}v_1=3\\v_{n+1}=v_n\end{matrix}\right.\)
\(\Rightarrow v_{n+1}=v_n=...=v_1=3\Rightarrow u_n=3-\frac{2}{2^n}\)
\(\Rightarrow u_{n-2}=3-\frac{2}{2^{n-2}}\Rightarrow lim\left(u_{n-2}\right)=lim\left(3-\frac{2}{2^{n-2}}\right)=3\)
Tính \(u_{n-2}\) hay \(u_n-2\) nhỉ? Ko dịch nổi nên đoán đại

Đáp án C
Ta có:
0 , 32111 . . . = 32 100 + 1 10 3 + 1 10 4 + 1 10 5 + . . . = 32 100 + 1 10 3 1 - 1 10 = 289 900 .
Vậy a = 289 , b = 900 . Do đó a - b = 289 - 900 = - 611 .

- Ta có:
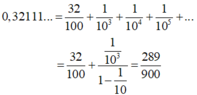
- Vậy a = 289, b = 900.
- Do đó: a - b = 289 – 900 = - 611.
Chọn B.
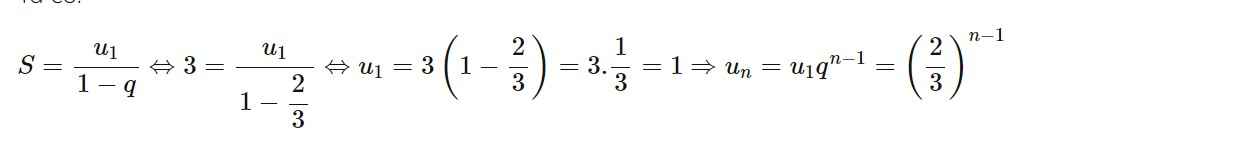
a: \(S=\dfrac{\dfrac{2}{3}}{\dfrac{5}{4}}=\dfrac{8}{15}\)
b: 1,(6)=5/3