VP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Gọi O là tâm đường tròn \(\Rightarrow\) O là trung điểm BC
\(\stackrel\frown{BE}=\stackrel\frown{ED}=\stackrel\frown{DC}\Rightarrow\widehat{BOE}=\widehat{EOD}=\widehat{DOC}=\dfrac{180^0}{3}=60^0\)
Mà \(OD=OE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow ED=R\)
\(BN=NM=MC=\dfrac{2R}{3}\Rightarrow\dfrac{NM}{ED}=\dfrac{2}{3}\)
\(\stackrel\frown{BE}=\stackrel\frown{DC}\Rightarrow ED||BC\)
Áp dụng định lý talet:
\(\dfrac{AN}{AE}=\dfrac{MN}{ED}=\dfrac{2}{3}\Rightarrow\dfrac{EN}{AN}=\dfrac{1}{2}\)
\(\dfrac{ON}{BN}=\dfrac{OB-BN}{BN}=\dfrac{R-\dfrac{2R}{3}}{\dfrac{2R}{3}}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{EN}{AN}=\dfrac{ON}{BN}=\dfrac{1}{2}\) và \(\widehat{ENO}=\widehat{ANB}\) (đối đỉnh)
\(\Rightarrow\Delta ENO\sim ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NBA}=\widehat{NOE}=60^0\)
Hoàn toàn tương tự, ta có \(\Delta MDO\sim\Delta MAC\Rightarrow\widehat{MCA}=\widehat{MOD}=60^0\)
\(\Rightarrow\Delta ABC\) đều
17 tháng 4 2017
Hướng dẫn trả lời:
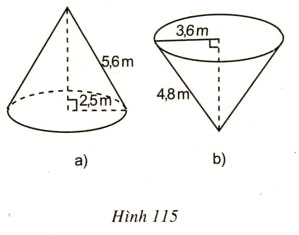
- Với hình a:
Stp = Sxq + Sđáy = πrl + πr2 = π . 2,5 . 5,6 + π . 2,52 = 63,69 (m2)
- Với hình b:
Stp = Sxq + Sđáy = π . 3,6 . 4,8 + π . 3,62 = 94,95 (m2)
9 tháng 6 2017
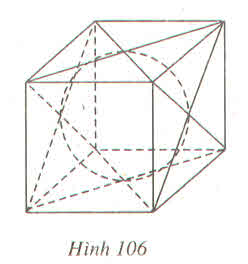
Ta thấy ngay cạnh của hình lập phương gấp đôi bán kính hình cầu
a) Tỉ số cần tính \(\dfrac{6}{\pi}\)
b) Diện tích toàn phần của hình lập phương là \(42cm^2\)
c) Thể tích cần tính xấp xỉ \(244cm^3\)
17 tháng 4 2017
Hướng dẫn trả lời:
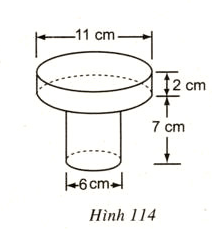
Ta có: Thể tích phần cần tính là tổng thể tích của hai hình trụ có đường kính là 11cm và chiều cao là 2cm.
V1=πR2h1=π(112)2.2=60,5π(cm3)V1=πR2h1=π(112)2.2=60,5π(cm3)
Thể tích hình trụ có đường kính đáy là 6cm, chiều cao là 7cm
V2=πR2h2=π(62)2.7=63π(cm3)V2=πR2h2=π(62)2.7=63π(cm3)
Vậy thể tích của chi tiết máy cần tính là:
V = V1 + V2 = 60,5π + 63 π = 123,5 π (cm3)
Tương tự, theo đề bài diện tích bề mặt của chi tiết máy bằng tổng diện tích xung quanh cua hai chi tiết máy.
Diện tích xung quanh của hình trụ có đường kính đáy 11 cm và chiều cao là 2cm là:
Sxq(1)=2πRh1=2π112.2=22π(cm2)Sxq(1)=2πRh1=2π112.2=22π(cm2)
Diện tích xung quanh của hình trụ có đường kính đáy là 6cm và chiều cao là 7cm là:
Sxq(2)=2πRh2=2π62.7=42π(cm2)Sxq(2)=2πRh2=2π62.7=42π(cm2)
Vậy diện tích bề mặt của chi tiết máy là:
S = Sxq(1) + Sxq(2) = 22π + 42π = 64π (cm2)
KS
0
13 tháng 7 2017
c)\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\)
=\(\dfrac{\sqrt{8-2\sqrt{7}}}{\sqrt{2}}-\dfrac{\sqrt{8+2\sqrt{7}}}{\sqrt{2}}\)
=\(\dfrac{\sqrt{\left(\sqrt{7}-1\right)^2}}{\sqrt{2}}-\dfrac{\sqrt{\left(\sqrt{7}+1\right)^2}}{\sqrt{2}}\)
=\(\dfrac{\left|\sqrt{7}-1\right|-\left|\sqrt{7}+1\right|}{\sqrt{2}}\)
=\(\dfrac{\sqrt{7}-1-\sqrt{7}-1}{\sqrt{2}}\)
=\(\dfrac{-2}{\sqrt{2}}\)
=\(-\sqrt{2}\)
17 tháng 4 2017
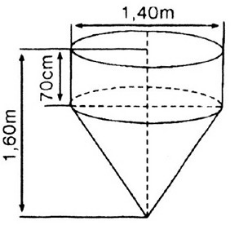
Giải: a) Thể tích cần tính gồm một hình trụ, đường kính đáy 1,4m, chiều cao 70cm, và một hình nón, bán kính đáy bằng bán kính hình trụ, chiều cao hình nón bằng 0,9m.
Thể tích hình trụ: Vtrụ = πR2h = 3,14. . 0.7 ≈ 1,077 (m3)
Thể tích hình nón: Vnón = (1/3). 3,14. .0,9 = 0,462 (m3)
Vậy thể tích cái phễu:
V = Vtrụ + Vnón = 1,077 + 0,462 = 1,539 (m3)
b) Diện tích cần tính gồm diện tích xung quanh hình trụ và diện tích xung quanh hình nón. Đường sinh của hình nón là:
Sxq trụ = 2πrh = 2.3,14.. 0,7= 3,077 (m2)
S xq nón = πrl = 3,14..1,4 = 2,506 (m2)
Vậy diện tích toàn phần của phễu:
S= Sxq trụ + S xq nón = 3,077 + 2,506 = 5,583 (m2)
a: Sxq=2*pi*r*l
=>2*pi*r*10=160pi
=>r=8
Stp=2*pi*8*(8+10)=288pi
b: V=pi*8^2*10=640pi