Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để thu gọn và sắp xếp các hạng tử của mỗi đa thức, ta cần thực hiện các bước sau:
Đối với đa thức P(x): P(x) = (4x + 1 - x^2 + 2x^3) - (x^4 + 3x - x^3 - 2x^2 - 5) = 4x + 1 - x^2 + 2x^3 - x^4 - 3x + x^3 + 2x^2 + 5 = -x^4 + 3x^3 + x^2 + x + 6
Đối với đa thức Q(x): Q(x) = 3x^4 + 2x^5 - 3x - 5x^4 - x^5 + x + 2x^5 - 1 = 2x^5 - x^5 + 3x^4 - 5x^4 + x - 3x - 1 = x^5 - 2x^4 - 2x - 1
Sau khi thu gọn và sắp xếp các hạng tử, ta có: P(x) = -x^4 + 3x^3 + x^2 + x + 6 Q(x) = x^5 - 2x^4 - 2x - 1
a: \(P\left(x\right)=\left(4x+1-x^2+2x^3\right)-\left(x^4+3x-x^3-2x^2-5\right)\)
\(=4x+1-x^2+2x^3-x^4-3x+x^3+2x^2+5\)
\(=-x^4+3x^3+x^2+x+6\)
\(Q\left(x\right)=3x^4+2x^5-3x-5x^4-x^5+x+2x^5-1\)
\(=\left(2x^5-x^5+2x^5\right)+\left(3x^4-5x^4\right)+\left(-3x+x\right)-1\)
\(=-x^5-2x^4-2x-1\)
b: Bạn ghi lại đề đi bạn

`a)`
\(P\left(x\right)=4x+3x^2+x^2+1-5x-2x\\ =\left(3x^2+x^2\right)+\left(4x-5x-2x\right)+1\\ =4x^2-3x+1\\ Q\left(x\right)=3x+x+7-5x^2+5x-11\\ =-5x^2+\left(3x+x+5x\right)+\left(7-11\right)\\ =-5x^2+9x-4\)
`b)`
Đa thức `P(x)` có :
Bậc `2`
Đa thức `Q(x)` có :
Bậc `2`
`c)`
\(P\left(x\right)+Q\left(x\right)=\left(4x^2-3x+1\right)+\left(-5x^2+9x-4\right)\\ =4x^2-3x+1-6x^2+9x-4\\ =\left(4x^2-5x^2\right)-\left(3x-9x\right)+\left(1-4\right)\\ =-x^2+6x-3\)
a: P(x)=4x^2+4x+1-7x=4x^2-3x+1
Q(x)=-5x^2+9x-4
b: P(x) có bậc 2
Q(x) có bậc 2
c: P(x)+Q(x)=4x^2-3x+1-5x^2+9x-4=-x^2+6x-3

Câu 80:
Tổng của 3 đơn thức đó là:
\(2^3x^2yz+2x^2yz+\left(-5x^2yz\right)\)
\(=8x^2yz+2x^2yz-5x^2yz\)
\(=\left(8+2-5\right).x^2yz\)
\(=5.x^2yz\)
\(=5x^2yz.\)
Câu 59:
\(P\left(x\right)=5x^3+2x^4-x^2-5x^3-x^4+1+3x^2+5x^2\)
\(\Rightarrow P\left(x\right)=\left(5x^3-5x^3\right)+\left(2x^4-x^4\right)-\left(x^2-3x^2-5x^2\right)+1\)
\(\Rightarrow P\left(x\right)=x^4-\left(-7x^2\right)+1\)
\(\Rightarrow P\left(x\right)=x^4+7x^2+1.\)
Vậy đa thức \(P\left(x\right)=x^4+7x^2+1.\)
Chúc bạn học tốt!

a) P(x) = -2x^2 + 4x^4 – 9x^3 + 3x^2 – 5x + 3
=4x^4-9x^3+x^2-5x+3
Q(x) = 5x^4 – x^3 + x^2 – 2x^3 + 3x^2 – 2 – 5x
=5x^4-3x^3+4x^2-5x-2
b)
P(x)
-bậc:4
-hệ số tự do:3
-hệ số cao nhất:4
Q(x)
-bậc :4
-hệ số tự do :-2
-hệ số cao nhất:5

a: \(P\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}\)
\(Q\left(x\right)=4x^4+2x^3-5x^2-6x+\dfrac{3}{2}\)
b: \(A\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}+4x^4+2x^3-5x^2-6x+\dfrac{3}{2}=-x^4+2x^3-3x^2-14x+2\)
\(B\left(x\right)=-5x^4+2x^2-8x+\dfrac{1}{2}-4x^4-2x^3+5x^2+6x-\dfrac{3}{2}=-9x^4-2x^3+7x^2-2x-1\)

`@` `\text {Ans}`
`\downarrow`
`a)`
`P(x) =`\(3x^2+7+2x^4-3x^2-4-5x+2x^3\)
`= (3x^2 - 3x^2) + 2x^4 + 2x^3 - 5x + (7-4)`
`= 2x^4 + 2x^3 - 5x + 3`
`Q(x) =`\(3x^3+2x^2-x^4+x+x^3+4x-2+5x^4\)
`= (5x^4 - x^4) + (3x^3 + x^3) + 2x^2 + (x + 4x)- 2`
`= 4x^4 + 4x^3 + 2x^2 + 5x - 2`
`b)`
`P(-1) = 2*(-1)^4 + 2*(-1)^3 - 5*(-1) + 3`
`= 2*1 + 2*(-1) + 5 + 3`
`= 2 - 2 + 5 + 3`
`= 8`
___
`Q(0) = 4*0^4 + 4*0^3 + 2*0^2 + 5*0 - 2`
`= 4*0 + 4*0 + 2*0 + 5*0 - 2`
`= -2`
`c)`
`G(x) = P(x) + Q(x)`
`=> G(x) = 2x^4 + 2x^3 - 5x + 3 + 4x^4 + 4x^3 + 2x^2 + 5x - 2`
`= (2x^4 + 4x^4) + (2x^3 + 4x^3) + 2x^2 + (-5x + 5x) + (3 - 2)`
`= 6x^4 + 6x^3 + 2x^2 + 1`
`d)`
`G(x) = 6x^4 + 6x^3 + 2x^2 + 1`
Vì `x^4 \ge 0 AA x`
`x^2 \ge 0 AA x`
`=> 6x^4 + 2x^2 \ge 0 AA x`
`=> 6x^4 + 6x^3 + 2x^2 + 1 \ge 0`
`=> G(x)` luôn dương `AA` `x`

a) \(P(x) = 4{x^2} + 1 + 3x = 4{x^2} + 3x + 1\) ; \(Q(x) = 5x + 2{x^2} + 3 = 2{x^2} + 5x + 3\).
b)
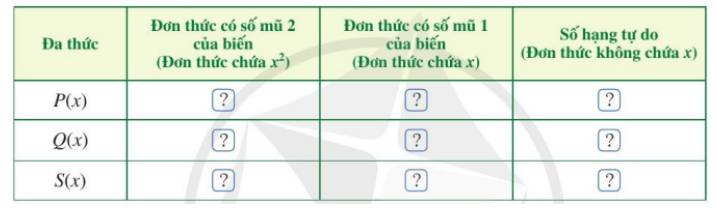
Đa thức | Đơn thức có số mũ 2 của biến (Đơn thức chứa \({x^2}\)) | Đơn thức có số mũ 1 của biến (Đơn thức chứa x) | Số hạng tự do (Đơn thức không chứa x) |
P(x) | \(4{x^2}\) | 3x | 1 |
Q(x) | \(2{x^2}\) | 5x | 3 |
S(x) | \(2{x^2}\) | – 2x | – 2 |
c) Vậy \(S(x) = 2{x^2} - 2x - 2\)

a: P(x)=-5x^3+6x^2+3x-1
Q(x)=-5x^3+6x^2+4x+2
b: H(x)=-5x^3+6x^2+3x-1-5x^3+6x^2+4x+2
=-10x^3+12x^2+7x+1
T(x)=-5x^3+6x^2+3x-1+5x^3-6x^2-4x-2
=-x-3
c: T(x)=0
=>-x-3=0
=>x=-3
d: G(x)=-(-10x^3+12x^2+7x+1)
=10x^3-12x^2-7x-1

a: P(x)=-x^3+2x^3-x^2+3x^2+x-1=x^3+2x^2+x-1
Q(x)=-3x^3+2x^3-x^2+3x-4x+3=-x^3-x^2-x+3
b: H(x)=P(x)+Q(X)
=x^3+2x^2+x-1-x^3-x^2-x+3
=x^2+2
c: H(-1)=H(1)=1+2=3
d: H(x)=x^2+2>=2>0 với mọi x
=>H(x) ko có nghiệm
a) Các đơn thức đồng dạng trong các đơn thức sau là: \(5x^2yz;-2x^2yz\) ; \(x^2yz\) ; \(0,2x^2yz\)
b) \(M\left(x\right)=3x^2+5x^3-x^2+x-3x-4\)
\(M\left(x\right)=(3x^2-x^2)+5x^3+(x-3x)-4\)
\(M\left(x\right)=2x^2+5x^3-2x-4\)
\(M\left(x\right)=5x^3+2x^2-2x-4\)
c) \(P+Q=\left(x^3x+3\right)+\left(2x^3+3x^2+x-1\right)\)
\(P+Q=x^3x+3+2x^3+3x^2+x-1\)
\(P+Q=\left(x^3+2x^3\right)+\left(x+x\right)+\left(3-1\right)+3x^2\)
\(P+Q=3x^3+2x+2+3x^2\)