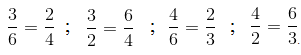Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Giả sử phân số \(\frac{6n-7}{n-1}\) chưa tối tối giản
=> 6n -7 và n - 1 có ước chung là số nguyên tố
Gọi d = ƯC(6n - 7; n - 1)
\(\Leftrightarrow\hept{\begin{cases}6n-7⋮d\\n-1⋮d\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}6n-7⋮d\\6n-6⋮d\end{cases}}\)
\(\Leftrightarrow1⋮d\)
Vì \(d\in N;1⋮d\Leftrightarrow d=1\)
\(\LeftrightarrowƯCLN\left(6n-7;n-1\right)=1\)

a) Gọi \(ƯCLN\left(15n+4;12n+3\right)\) là \(d\) .
\(\Leftrightarrow\left\{{}\begin{matrix}15n+4⋮d\\12n+3⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4\left(15n+4\right)⋮d\\5\left(12n+3\right)⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}60n+16⋮d\\60n+15⋮d\end{matrix}\right.\)
\(\Leftrightarrow\left(60n+16\right)-\left(60n+15\right)⋮d\)
\(\Leftrightarrow60n+16-60n-15⋮d\)
\(\Leftrightarrow1⋮d\)
\(\Leftrightarrow d=1\)
Vậy phân số \(\dfrac{15n+4}{12n+3}\) là phân số tối giản với \(n\in N\).
b) Từ đẳng thức \(\left(-5\right).9=3.\left(-10\right)\) ta lập được các cặp phân số bằng nhau:
\(\dfrac{-5}{3}=\dfrac{-10}{9}\)
\(\dfrac{-5}{-10}=\dfrac{3}{9}\)
\(\dfrac{9}{3}=\dfrac{-10}{-5}\)
\(\dfrac{9}{-10}=\dfrac{3}{-5}\)

Giải:
Các cặp phân số bằng nhau lập được từ đẳng thưc 3.4 = 6.2 là :
\(\frac{3}{6}=\frac{2}{4}\); \(\frac{6}{2}=\frac{4}{2}\); \(\frac{4}{6}=\frac{2}{3}\); \(\frac{3}{2}=\frac{6}{4}\)
Vậy ...

Ta có :
-2/4 = 7/-14
4/-2 = -14/7
-2/7 = -4/14
7/-2 = 14/-4

Gọi ƯCLN (n;n+1) = d ( d \(\in\)N*)
\(\left\{{}\begin{matrix}n⋮d\\n+1⋮d\end{matrix}\right.\Rightarrow n+1-n⋮d\Leftrightarrow1⋮d\Leftrightarrow d=1\)
Vậy ta có đpcm

Gọi d là (2n+5;3n+7)
\(\Rightarrow\hept{\begin{cases}2n+5⋮d\\3n+7⋮d\end{cases}}\Leftrightarrow\hept{\begin{cases}3\left(2n+5\right)⋮d\\2\left(3n+7\right)⋮d\end{cases}}\Leftrightarrow\hept{\begin{cases}6n+15⋮d\\6n+14⋮d\end{cases}}\)
=> [6n+15 - ( 6n+14 )] \(⋮\) d
=> 1 \(⋮\)d
=> phân số trên tối giản