Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

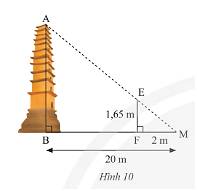
Xét \(\Delta MEF\) và \(\Delta MAB\) có:
\(\widehat M\) chung
\(\widehat {MFE} = \widehat {MBA} = 90^\circ \)
Do đó, \(\Delta MEF\backsim\Delta MAB\) (g.g)
Vì nên \(\frac{{MF}}{{MB}} = \frac{{FE}}{{AB}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{2}{{20}} = \frac{{1,65}}{{AB}} \Rightarrow AB = \frac{{1,65.20}}{2} = 16,5\)
Vậy tòa tháp cao 16,5m.

- Có AB // CD
=> \(\widehat {BAC} = \widehat {DCA}\) (2 góc so le trong)
\(\widehat {BDC} = \widehat {AB{\rm{D}}}\)(2 góc so le trong)
- Xét hai tam giác ABE và tam giác CDE, có \(\widehat {BAC} = \widehat {DCA};\widehat {B{\rm{D}}C} = \widehat {AB{\rm{D}}}\)
=> ΔABE ∽ ΔCDE
=> \(\frac{{C{\rm{D}}}}{{AB}} = \frac{{CE}}{{A{\rm{E}}}} = \frac{2}{3}\)
=> \(\frac{{CE}}{{A{\rm{E}}}} = \frac{2}{3}\)=> \(\frac{{CE}}{{CA}} = \frac{2}{5}\)
- Xét hai tam giác CEF và tam giác CAB có EF // AB
=> ΔCEF ∽ ΔCAB (theo định lý)
=> \(\frac{{F{\rm{E}}}}{{AB}} = \frac{{CE}}{{CA}} = \frac{2}{5}\)
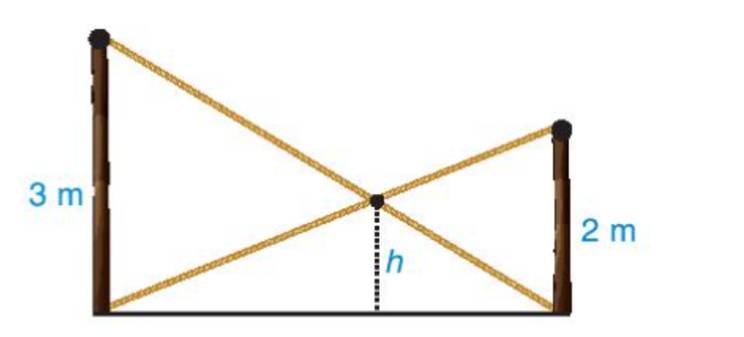
=> \(\frac{{F{\rm{E}}}}{{AB}} = \frac{2}{5}\) => \(\frac{{F{\rm{E}}}}{3} = \frac{2}{5}\)=> \(F{\rm{E}} = 3.\frac{2}{5} = 1,2(m)\)
Vậy độ cao h là 1,2 m

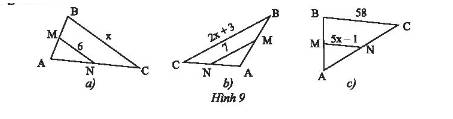
- Hình a:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}x \Leftrightarrow 6 = \frac{1}{2}x \Leftrightarrow x = 6:\frac{1}{2} = 12\)
- Hình b:
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\(\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow 7 = \frac{1}{2}\left( {x + 3} \right) \Leftrightarrow \left( {x + 3} \right) = 7:\frac{1}{2} = 14\)
\( \Rightarrow x = 14 - 3 \Leftrightarrow x = 11\).
- Hình c
Vì \(MN\) là đường trung bình của tam giác \(ABC\) nên theo tính chất đường trung bình ta có:
\[\left\{ \begin{array}{l}MN//BC\\MN = \frac{1}{2}BC\end{array} \right. \Rightarrow MN = \frac{1}{2}.58 \Leftrightarrow \left( {5x - 1} \right) = \frac{1}{2}.58\]
\[ \Leftrightarrow \left( {5x - 1} \right) = 29 \Leftrightarrow 5x = 30 \Leftrightarrow x = 30:5 \Leftrightarrow x = 6\].
a: MN là đường trung bình
=>MN=BC/2
=>x=6*2=12
b: MN là đường trung bình
=>2x+3=2*7=14
=>2x=11
=>x=11/2
c: MN là đường trung bình
=>5x-1=58/2=29
=>5x=30
=>x=6

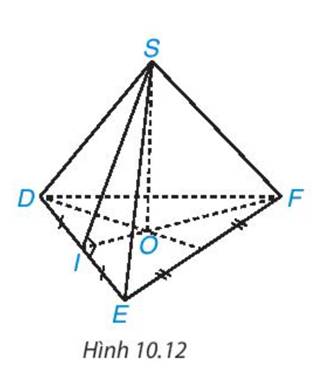
- Đỉnh: S
- Cạnh bên: SD, SE, SF
- Mặt bên: SDE, SEF, SDF
- Mặt đáy: DEF
- Đường cao: SO
- Một trung đoạn: SI

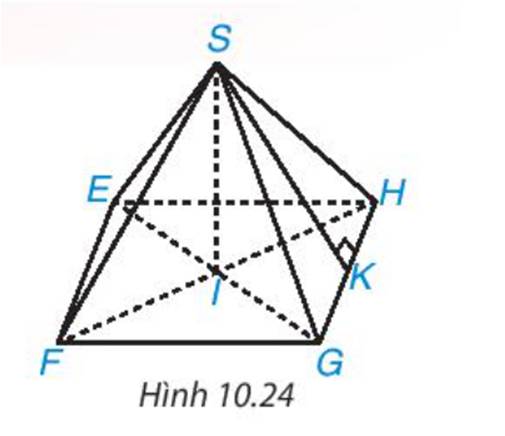
- Đỉnh: S
- Cạnh bên: SE, SF, SG, SH
- Mặt bên: SEF, SFG, SGH. SEH
- Mặt đáy: EFGH
- Đường cao: SI
- Một trung đoạn: SK

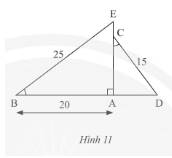
Xét \(\Delta ABE\) và \(\Delta ACD\) có:
\(\widehat {EBA} = \widehat {ACD}\) (giả thuyết)
\(\widehat {BAE} = \widehat {CAD} = 90^\circ \)
Do đó, \(\Delta ABE\backsim\Delta ACD\) (g.g)
Vì \(\Delta ABE\backsim\Delta ACD\) nên \(\frac{{AB}}{{AC}} = \frac{{EB}}{{CD}}\) (các cặp cạnh tương ứng)
Thay số, \(\frac{{20}}{{AC}} = \frac{{25}}{{15}} \Rightarrow AC = \frac{{20.15}}{{25}} = 12\)cm.
Áp dụng định lí Py – ta – go cho \(\Delta ABE\) vuông tại \(A\) ta có:
\(B{E^2} = A{E^2} + A{B^2} \Leftrightarrow A{E^2} = B{E^2} - A{B^2} = {25^2} - {20^2} = 225 \Rightarrow AE = \sqrt {225} = 15\)cm.
Độ dài \(CE\) là:
15 – 12 = 3cm
Vậy \(CE = 3cm.\)

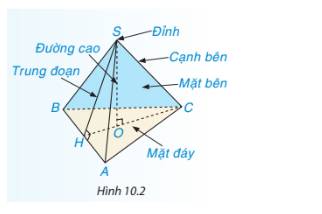
Hình chóp tam giác đều S. ABC có:
- Đỉnh: S
- Cạnh bên: SA, SB, SC.
- Mặt đáy: tam giác ABC.
- Đường cao: SO.
- Trung đoạn: SH

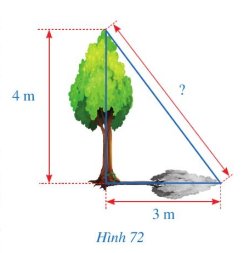
Khoảng cách từ điểm xa nhất của bóng cây đến đỉnh cây bằng \(\sqrt{3^2+4^2}=5\left(m\right)\) (áp dụng định lý Py-ta-go).




a: Xét ΔABC có DE//BC
nên AN/AB=AM/AC
=>1,5/AB=2,4/5,3
=>\(AB\simeq3,3125\left(m\right)\)
b:
Xét ΔABC có DE//BC
nên DE/BC=AE/AC=(AC-CE)/AC
=>36-x=1,6*36/24=2.4
=>x=33,6(m)
a) Xét tam giác \(ABC\) có \(MN//BC\) nên theo định lí Thales ta có:
\(\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} \Leftrightarrow \frac{{1,5}}{{AB}} = \frac{{2,4}}{{2,4 + 2,9}} \Rightarrow AB = \frac{{1,5.\left( {2,4 + 2,9} \right)}}{{2,4}} = 3,3125\)
Vậy chiều cao \(AB\)của cái cây là 3,3125m.
b) Đặt tên các điểm như hình vẽ
Xét tam giác \(ABC\) có \(DE//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{DE}}{{BC}} = \frac{{AE}}{{AC}} = \frac{{AC - CE}}{{AC}} \Leftrightarrow \frac{{1,6}}{{24}} = \frac{{36 - x}}{{36}}\)
\( \Rightarrow 36 - x = \frac{{1,6.36}}{{24}} \Leftrightarrow x = 36 - \frac{{1,6.36}}{{24}} = 33,6\)
Vậy người đó có thể đứng xa tòa nhà nhất là 33,6m.