Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\forall\)n \(\in\) N* ta có :
\(\dfrac{1}{n\left(n+1\right)}=\dfrac{n+1-n}{n\left(n+1\right)}=\dfrac{n+1}{n\left(n+1\right)}=\dfrac{1}{n}-\dfrac{1}{n+1}\) (đpcm)

Ta có:
Mà a = b + c nên
Từ (1), (2) suy ra:
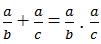

Bài 2 : đề bài này chỉ cần a,b>0 , ko cần phải thuộc N* đâu
a, Áp dụng bất đẳng thức AM-GM cho 2 số lhoong âm a,b ta được :
\(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ba}}=2\) . Dấu "=" xảy ra khi a=b
b , Áp dụng BĐT AM-GM cho 2 số không âm ta được : \(a+b\ge2\sqrt{ab}\)
\(\dfrac{1}{a}+\dfrac{1}{b}\ge2\sqrt{\dfrac{1}{ab}}=\dfrac{2}{\sqrt{ab}}\)
Nhân vế với vế ta được :
\(\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge2.2.\dfrac{\sqrt{ab}}{\sqrt{ab}}=4\left(đpcm\right)\)
Dấu "="xảy ra tại a=b
Bài 1.
Vì a, b, c, d \(\in\) N*, ta có:
\(\dfrac{a}{a+b+c+d}< \dfrac{a}{a+b+c}< \dfrac{a}{a+b}\)
\(\dfrac{b}{a+b+c+d}< \dfrac{b}{a+b+d}< \dfrac{b}{a+b}\)
\(\dfrac{c}{a+b+c+d}< \dfrac{c}{b+c+d}< \dfrac{c}{c+d}\)
\(\dfrac{d}{a+b+c+d}< \dfrac{d}{a+c+d}< \dfrac{d}{c+d}\)
Do đó \(\dfrac{a}{a+b+c+d}+\dfrac{b}{a+b+c+d}+\dfrac{c}{a+b+c+d}+\dfrac{d}{a+b+c+d}< M< \left(\dfrac{a}{a+b}+\dfrac{b}{a+b}\right)+\left(\dfrac{c}{c+d}+\dfrac{d}{c+d}\right)\)hay 1<M<2.
Vậy M không có giá trị là số nguyên.
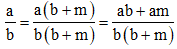
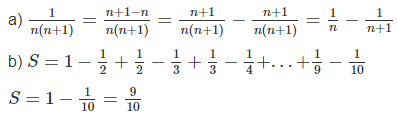
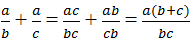
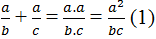
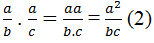
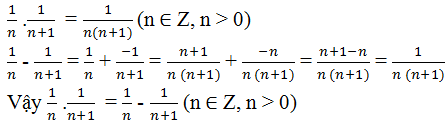

So sánh: \(\dfrac{434}{561}\) và \(\dfrac{441}{568}\)
* Bài làm:
Vì \(\dfrac{434}{561}\) < 1 => \(\dfrac{434}{561}\) < \(\dfrac{434+7}{561+7}\) hay \(\dfrac{434}{561}\) < \(\dfrac{441}{568}\)
a) \(\dfrac{a}{b}\)=\(\dfrac{a\left(b+m\right)}{b\left(b+m\right)}\)=\(\dfrac{ab+am}{b^2+bm}\) ; (1)
\(\dfrac{a+m}{b+m}\)=\(\dfrac{b\left(a+m\right)}{b\left(b+m\right)}\)=\(\dfrac{ab+bm}{b^2+bm}\) ; (2)
\(\dfrac{a}{b}\) < \(1\) \(\Rightarrow\) \(a\) < \(b\), suy ra \(ab+am\) < \(ab+bm\). (3)
Từ (1), (2) và (3) ta có: \(\dfrac{a}{b}\) < \(\dfrac{a+m}{b+m}\)
b) Áp dụng, rõ ràng \(\dfrac{434}{561}\) < 1 nên \(\dfrac{434}{561}\) < \(\dfrac{434+7}{561+7}\)=\(\dfrac{441}{568}\)