Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét hai tam giác ABC và CDA có:AB = CD; AD = BC; AC chung nên \(\Delta ABC = \Delta C{\rm{D}}A(c - c - c)\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CAD}\).
Nên ABCD hình bình hành.
b) Xét hai tam giác ABO và tam giác CDO có: \(OA = OB;\widehat {AOB} = \widehat {CO{\rm{D}}};OC = O{\rm{D}}\)
Suy ra: \(\Delta ABO = \Delta C{\rm{D}}O\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CA{\rm{D}}}\).
Nên ABCD là hình bình hành.

a, Hình chữ nhật ABCD có AB = BC
Suy ra hình chữ nhật ABCD có \(\widehat A = \widehat B = \widehat C = \widehat D = {90^0};AB = BC = CD = DA\)
Suy ra hình chữ nhật ABCD là hình vuông
b, O là giao điểm của AC và BD.
Vì ABCD là hình chữ nhật nên OB = OD.
Mà AC vuông góc BD. Suy ra AC là đường trung trực của đoạn thẳng BD.
Xét \(\Delta ABD\) có AO vừa là đường trung trực vừa là đường cao
\( \Rightarrow \Delta ABD \) là tam giác vuông cân tại A.
\( \Rightarrow AB = AD\)
Mà AB = CD, AD = BC (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.
c, Ta có ABCD là hình chữ nhật nên \(\widehat A =\widehat B = \widehat C = \widehat D = 90^0\)
Vì AC là tia phân giác của góc DAB nên ta có: \(\widehat{DAC} = \widehat{CAB} =\frac{\widehat{DAB}}{2} = \frac{90^0}{2} = 45^0\)
Xét tam giác ABC vuông tại B (\(\widehat B = 90^0\)), ta có:
\(\widehat{ACB} + \widehat B + \widehat{CAB} = 180^0\)
\(\Rightarrow \widehat{ACB} = 180^0 - \widehat B - \widehat{CAB} = 180^0 - 90^0 - 45^0 = 45^0\)
\( \Rightarrow \widehat{ACB} = \widehat{CAB} =45^0\) nên tam giác ABC vuông cân tại B.
\( \Rightarrow AB = BC\)
Mà AB = CD, BC = AD (tính chất hình chữ nhật)
\(\Rightarrow AB = BC = CD = DA\) nên ABCD là hình vuông.

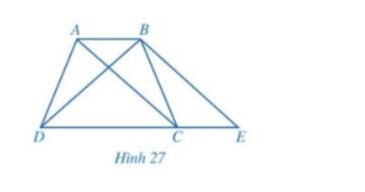
Do ABCD là hình thang nên AB//CD.
Kẻ BE//AC, \(E \in CD\) nên CE//AB.
\( \Rightarrow \widehat {BCE} = \widehat {ABC}\); \(\widehat {CBE} = \widehat {ACB}\) (hai góc so le trong).
a, Xét \(\Delta ABC\)và \(\Delta ECB\) có:
\(\widehat {BCE} = \widehat {ABC}\)
BC chung
\(\widehat {CBE} = \widehat {ACB}\) (do BC//AC )
\( \Rightarrow \Delta ABC = \Delta ECB\)(g.c.g)
b, BE = AC = BD
\( \Rightarrow \Delta BDE\)cân tại B
\( \Rightarrow \widehat {BDE} = \widehat {BED}\)
Do \(\Delta ABC = \Delta ECB\)
\( \Rightarrow \widehat {BEC} = \widehat {BAC}\) (2 góc tương ứng) hay \(\widehat {BED} = \widehat {BAC}(1)\)
Mà: \(\widehat {BAC} = \widehat {ACD}\) (do AB//CD) (2)
Từ (1), (2) suy ra: \(\widehat {BED} = \widehat {ACD}\)
c, Theo câu b:
\(\begin{array}{l}\widehat {BED} = \widehat {BDE}\\\widehat {ACD} = \widehat {BED}\end{array}\) suy ra: \(\widehat {ACD} = \widehat {BDE}\) hay \(\widehat {ACD} = \widehat {BDC}\)
Xét \(\Delta ACD\)và \(\Delta BDC\)có:
CD chung
\(\widehat {ACD} = \widehat {BDC}\)
AC = BD (gt)
\( \Rightarrow \Delta ACD = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {ADC} = \widehat {BCD}\) (2 góc tương ứng)
d, Hình thang ABCD (AB//CD) có \(\widehat {ADC} = \widehat {BCD}\)nên hình thang ABCD là hình thang cân.

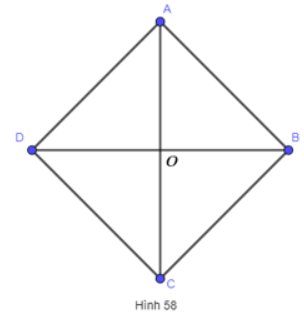
a) Hình thoi ABCD có là hình bình hành (vì AB = BC = CD = DA)
b) Xét tam giác ABD có AB = AD nên tam giác ABD là tam giác cân tại A.
Suy ra đường trung tuyến AO đồng thời là đường cao.
Suy ra AO vuông góc với BD
Hay AC vuông góc với BD
c) Xét tam giác ABC và tam giác ADC có:
AD = AB
CD = CB
AC chung
\(\begin{array}{l}\Delta ABC = \Delta A{\rm{D}}C\\ \Rightarrow \widehat {DAC} = \widehat {BAC}\end{array}\)
Mà AC nằm giữa 2 tia AB và AD
Suy ra: AC là tia phân giác của góc BAD

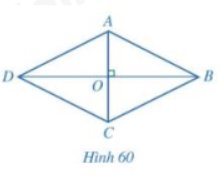
a) Hình bình hành ABCD có AB = BC
Suy ra: AB = BC = CD = DA
Nên hình bình hành ABCD là hình thoi
b) AC giao điểm với BD tại O
Ta có: O là trung điểm của BD (do ABCD là hình bình hành)
AO vuông góc với BD
Suy ra AO là đường trung trực của đoạn thẳng BD
Suy ra tam giác ABD cân tại A
Suy ra: AB = AD
Suy ra AB = DC = AD = BC
Hình bình hành ABCD là hình thoi

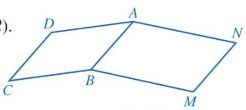
a, Do ABCD là hình bình hành: AB = CD.
Do ABMN là hình bình hành: AB = MN
Suy ra: CD = MN = AB
b, Do ABCD là hình bình hành \( \Rightarrow \widehat {BCD} = \widehat {DAB}\)
Do ABMN là hình bình hành \( \Rightarrow \widehat {BMN} = \widehat {NAB}\)
\(\widehat {BCD} + \widehat {BMN} = \widehat {DAB} + \widehat {NAB} = \widehat {DAN}\)

a) Xét tam giác ABD và tam giác CDB có:
\(\widehat {ABD} = \widehat {CDB}\) ( vì AB //CD)
BD chung
\(\widehat {ADB} = \widehat {CBD}\) (vì AD // BC)
Suy ra: \(\Delta ABD = \Delta CDB\)(g - c - g)
Suy ra: AB = CD, DA = BC.
b) Vì \(\Delta AB{\rm{D}} = \Delta C{\rm{D}}B\) (g - c - g) suy ra: \(\widehat {DAB}\) = \(\widehat {BCD}\)
Xét tam giác ABC và tam giác CDA có:
AB = CD (cmt)
Cạnh AC chung
BC = AD (cmt)
\(\Delta ABC = \Delta CDA (c - c - c) \Rightarrow \widehat {ABC} = \widehat {CDA}\) (2 góc tương ứng)
c) Xét tam giác OAB và OCD có:
\(\begin{array}{l}\widehat {OAB} = \widehat {OCD} (cmt)\\AB = CD (cmt)\\\widehat {OBA} = \widehat {ODC} (cmt)\end{array}\)
Suy ra: \(\Delta OAB = \Delta OC{\rm{D}}\) (g - c - g) suy ra: OA = OC; OB = OD (các cạnh tương ứng)




a) Hình bình hành ABCD có \(\widehat A = {90^o}\)
Suy ra: \(\widehat C = \widehat A = {90^o}\)
Suy ra: \(\widehat B = \widehat D = \dfrac{{{{360}^o} - \widehat A - \widehat C}}{2} = \dfrac{{{{360}^o} - {{90}^o} - {{90}^o}}}{2} = {90^o}\)
Vậy ABCD là hình chữ nhật
b) Xét hai tam giác ABC và tam giác DCB có:
BC chung
AB = DC
AC = BD
Suy ra: \(\Delta ABC = \Delta DCB \Rightarrow \widehat {ABC} = \widehat {DCB}\)
Suy ra: \(\widehat {ABC} = \widehat {DCB} = \widehat {ADC} = \widehat {DAB} = {360^o}:4 = {90^o}\)
Vậy ABCD là hình chữ nhật.