Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quãng đường đi được = Khoảng cách từ vị trí đầu đến vị trí cuối trong quá trình chuyển động.
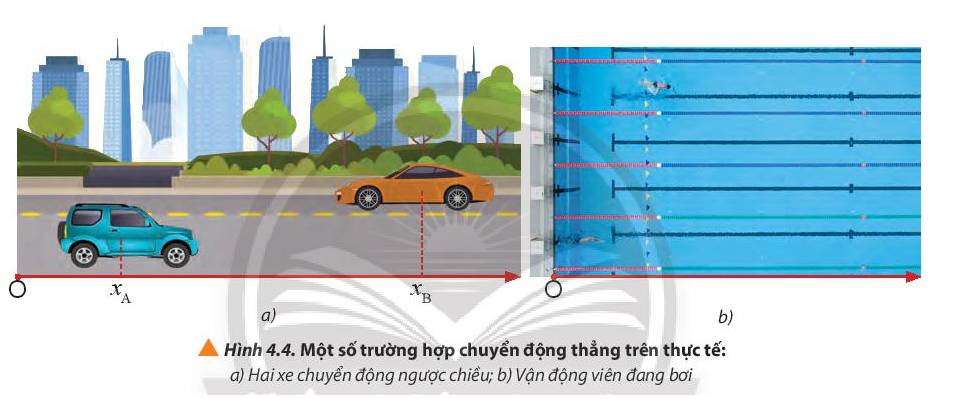
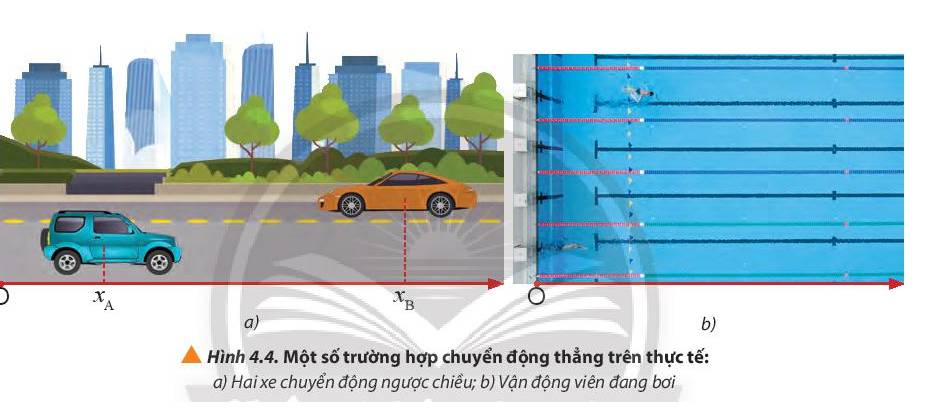
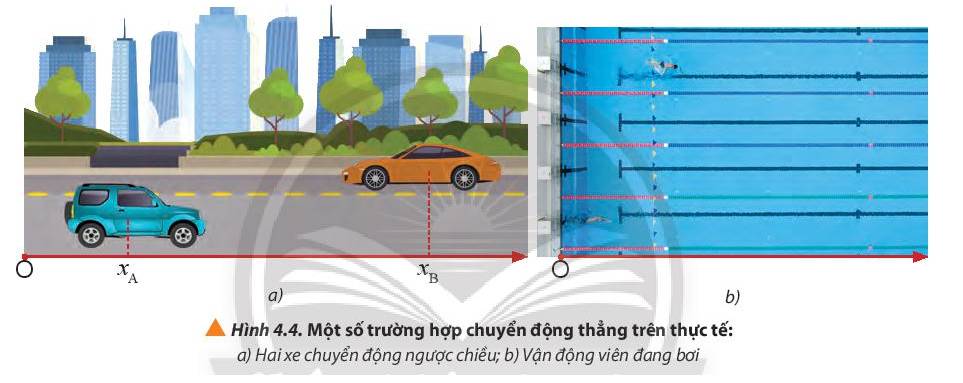
Chiều chuyển động của hai xe trong hình 4.4a:
+ Xe A chuyển động theo chiều dương
+ Xe B chuyển động ngược chiều dương
Chiều chuyển động của vận động viên bơi; Vận động viên bơi theo chiều dương.

- Tình huống 1 (Hình 4.4a)
+ Quãng đường đi được của hai xe là: sA = sB = xB – xA
+ Độ dịch chuyển của xe A: dA = xB – xA
+ Độ dịch chuyển của xe B: dB = xA – xB
- Tình huống 2 (Hình 4.4b)
+ Quãng đường và độ dịch chuyển của vận động bằng nhau và đều bằng l

- Tình huống 1 (Hình 4.4a)
+ Quãng đường đi được của hai xe là: sA = sB = xB – xA
+ Độ dịch chuyển của xe A: dA = xB – xA
+ Độ dịch chuyển của xe B: dB = xA – xB
- Tình huống 2 (Hình 4.4b)
+ Quãng đường và độ dịch chuyển của vận động bằng nhau và đều bằng l.

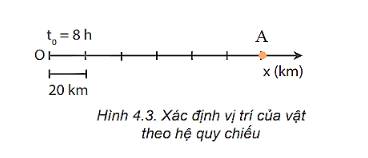
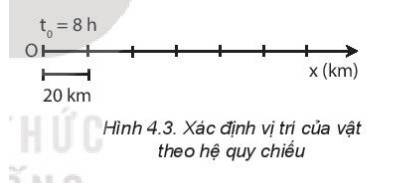
- Thời gian chuyển động của vật A là: t = t’- t0 = 11 – 8 = 3 h
- Quãng đường mà vật A đi được là: s = v.t = 40.3 = 120 km
- Vị trí của vật A trên trục Ox vẽ ở Hình 4.3 tại thời điểm 11 h: nằm trên trục Ox cách gốc tọa độ O 120 km.

Do vận động viên bơi không đổi chiều chuyển động nên độ dịch chuyển bằng quãng đường
=> Vận tốc trung bình = Tốc độ trung bình = \(\dfrac{l}{t}\)

Do vận động viên bơi không đổi chiều chuyển động nên độ dịch chuyển bằng quãng đường
=> Vận tốc trung bình = Tốc độ trung bình = l/t

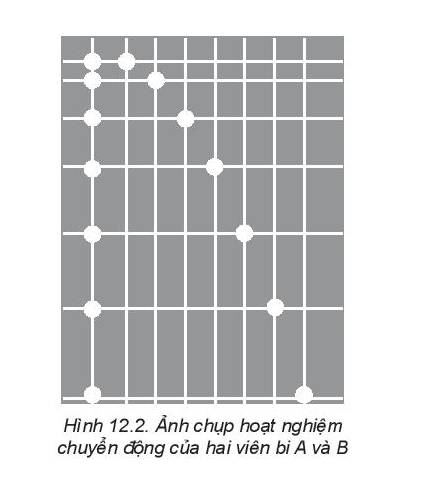
Thông qua quan sát, ta thấy tọa độ tính theo phương ngang của hai viên bi A và viên bi B đều không thay đổi, và đều trong cùng một khoảng thời gian
Mặt khác, ta có \(v=\dfrac{s}{t}=\dfrac{x}{t}\)
(do vật không đổi chiều chuyển động). Tọa độ x không đổi, thời gian như nhau, nên vận tốc không thay đổi
\(\Rightarrow v_x=v_0\)
Khi xe mô tô đua vào khúc cua thì bộ phận của xe chuyển động tròn là: bánh xe.

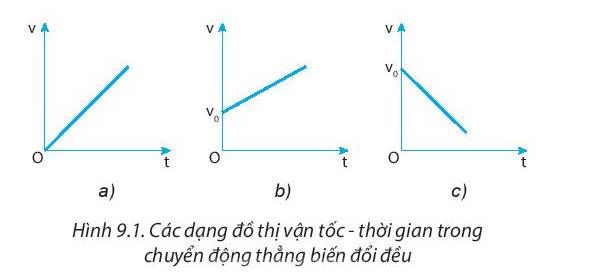
1. (a)
Đồ thị hình a là đường thẳng đi qua gốc tọa độ nên công thức mối liên hệ giữa v, a và t có dạng hàm số \(y=ax\). Công thức cần tìm là: \(v=at\left(a>0\right)\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a>0\right)\) (do đồ thị có dạng dấu sắc (đồng biến)) nên công thức cần tìm là: \(v=v_0+at\).
Đồ thị hình b là đường thẳng xuất phát từ điểm \(v_0\) cách gốc tọa độ một khoảng đúng bằng \(v_0\) nên công thức mối liên hệ có dạng hàm số \(y=ax+b\left(a< 0\right)\) (do đồ thị có dạng dấu huyền (nghịch biến)) nên công thức cần tìm là: \(v=v_0-at\).
(b) Chuyển động nhanh dần đều là các chuyển động ở hình a, b. Chuyển động chậm dần đều là chuyển động ở hình c.
2. Từ thời điểm 0s đến 4s, tức 4s đầu, bạn đi đều với tốc độ 1,5m/s.
Từ thời điểm 4s đến 6s, tức 2s tiếp theo, bạn bắt đầu đi chậm lại từ tốc độ 1,5m/s xuống 0m/s.
Sau đó, từ thời điểm 6s đến 7s, tức 1s tiếp theo, bạn này dừng lại.
Trong 1s tiếp theo, từ thời điểm 7s đến 8s, bạn này bắt đầu đảo chiều đi (đi ngược lại so với chiều đi ban đầu) và bắt đầu chuyển động nhanh dần từ tốc độ 0m/s đến 0,5m/s.
Trong 1s sau đó, từ thời điểm 8s đến 9s, bạn này đi đều với tốc độ 0,5m/s với chiều đi như giây trước.
Cuối cùng, từ thời điểm 9s đến 10s, tức 1s cuối, bạn này đi chậm lại từ tốc độ 0,5m/s và dừng hẳn (tốc độ 0m/s).




Quãng đường đi được = Khoảng cách từ vị trí đầu đến vị trí cuối trong quá trình chuyển động.
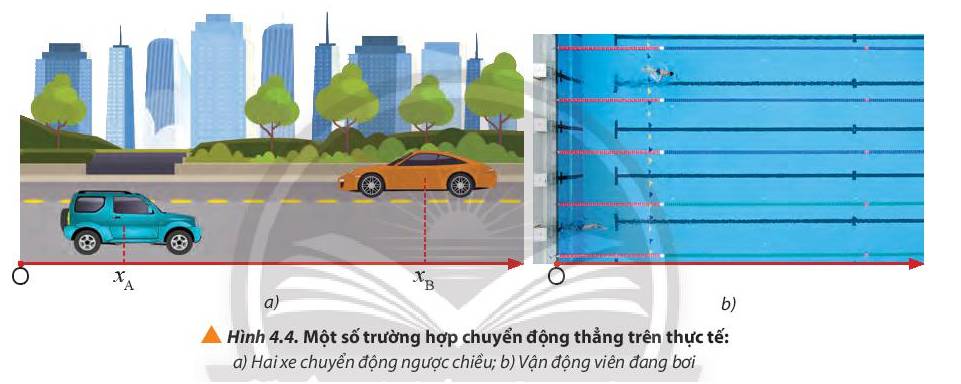
Chiều chuyển động của hai xe trong hình 4.4a:
+ Xe A chuyển động theo chiều dương
+ Xe B chuyển động ngược chiều dương
Chiều chuyển động của vận động viên bơi; Vận động viên bơi theo chiều dương.