K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
N
2
S
18 tháng 3 2020
\(\frac{2}{3x}=\frac{3}{4y}=\frac{5}{6z}\Rightarrow\frac{2}{30.3x}=\frac{3}{30.4y}=\frac{5}{30.6z}\Leftrightarrow\frac{1}{45x}=\frac{1}{40y}=\frac{1}{36z}\Rightarrow45x=40y=36z\)
\(\Rightarrow x=\frac{9}{8}y;x=\frac{5}{4}z\Rightarrow x^2+y^2+z^2=x^2+\frac{64}{81}x^2+\frac{16}{25}x^2\)
\(=x^2\left(1+\frac{2896}{2025}\right)=724\text{ :)) đến đây thôi :))}\)
20 tháng 9 2019
\(a,4x=5y\:\Rightarrow\frac{x}{5}=\frac{y}{4}\Rightarrow\frac{x}{15}=\frac{y}{12}\)
\(4y=6z\Rightarrow\frac{y}{6}=\frac{z}{4}\Rightarrow\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\frac{x}{15}=\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\frac{x}{15}=\frac{2y}{24}=\frac{3z}{24}\)
\(\Rightarrow\frac{x-2y+3z}{15-24+24}=\frac{x}{15}=\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\frac{5}{15}=\frac{x}{15}=\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\frac{1}{3}=\frac{x}{15}=\frac{y}{12}=\frac{z}{8}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{1}{3}\cdot15=5\\y=\frac{1}{3}\cdot12=4\\z=\frac{1}{3}\cdot8=\frac{8}{3}\end{cases}}\)
TP
7 tháng 8 2017
Ta có:
a) \(\frac{x}{4}=\frac{y}{3}=\frac{z}{5}\) và \(x+y+z=552\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{4}=\frac{y}{3}=\frac{z}{5}=\frac{x+y+z}{4+3+5}=\frac{552}{12}=46\)
\(\hept{\begin{cases}\frac{x}{4}=46\Rightarrow x=46.4=184\\\frac{y}{3}=46\Rightarrow y=46.3=138\\\frac{z}{5}=46\Rightarrow z=46.5=230\end{cases}}\)
Vậy ..........................................
TP
7 tháng 8 2017
b)
Ta có:
\(3x=4y=6z\Leftrightarrow\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{4}}=\frac{z}{\frac{1}{6}}\) và \(x+y+z=315\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{4}}=\frac{z}{\frac{1}{6}}=\frac{x+y+z}{\frac{1}{3}+\frac{1}{4}+\frac{1}{6}}=\frac{315}{\frac{3}{4}}=420\)
\(\hept{\begin{cases}\frac{x}{\frac{1}{3}}=420\Rightarrow x=\frac{1}{3}.420=140\\\frac{y}{\frac{1}{4}}=420\Rightarrow y=\frac{1}{4}.420=105\\\frac{z}{\frac{1}{6}}=420\Rightarrow z=\frac{1}{6}.420=70\end{cases}}\)
Vậy ......................................
DD
0
MH
1
5 tháng 10 2019
Ta có: 3x = 4y => \(\frac{x}{4}=\frac{y}{3}\) => \(\frac{x}{8}=\frac{y}{6}\)
5y = 6z => \(\frac{y}{6}=\frac{z}{5}\)
=> \(\frac{x}{8}=\frac{y}{6}=\frac{z}{5}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{8}=\frac{y}{6}=\frac{z}{5}=\frac{x+y-z}{8+6-5}=\frac{18}{9}=2\)
=> \(\hept{\begin{cases}\frac{x}{8}=2\\\frac{y}{6}=2\\\frac{z}{5}=2\end{cases}}\) => \(\hept{\begin{cases}x=2.8=16\\y=2.6=12\\z=2.5=10\end{cases}}\)
Vậy ....
20 tháng 8 2021
Lần sau bạn nhớ đánh đề rõ ràng hơn. Nếu nhìn đề thì mình nghĩ thế này
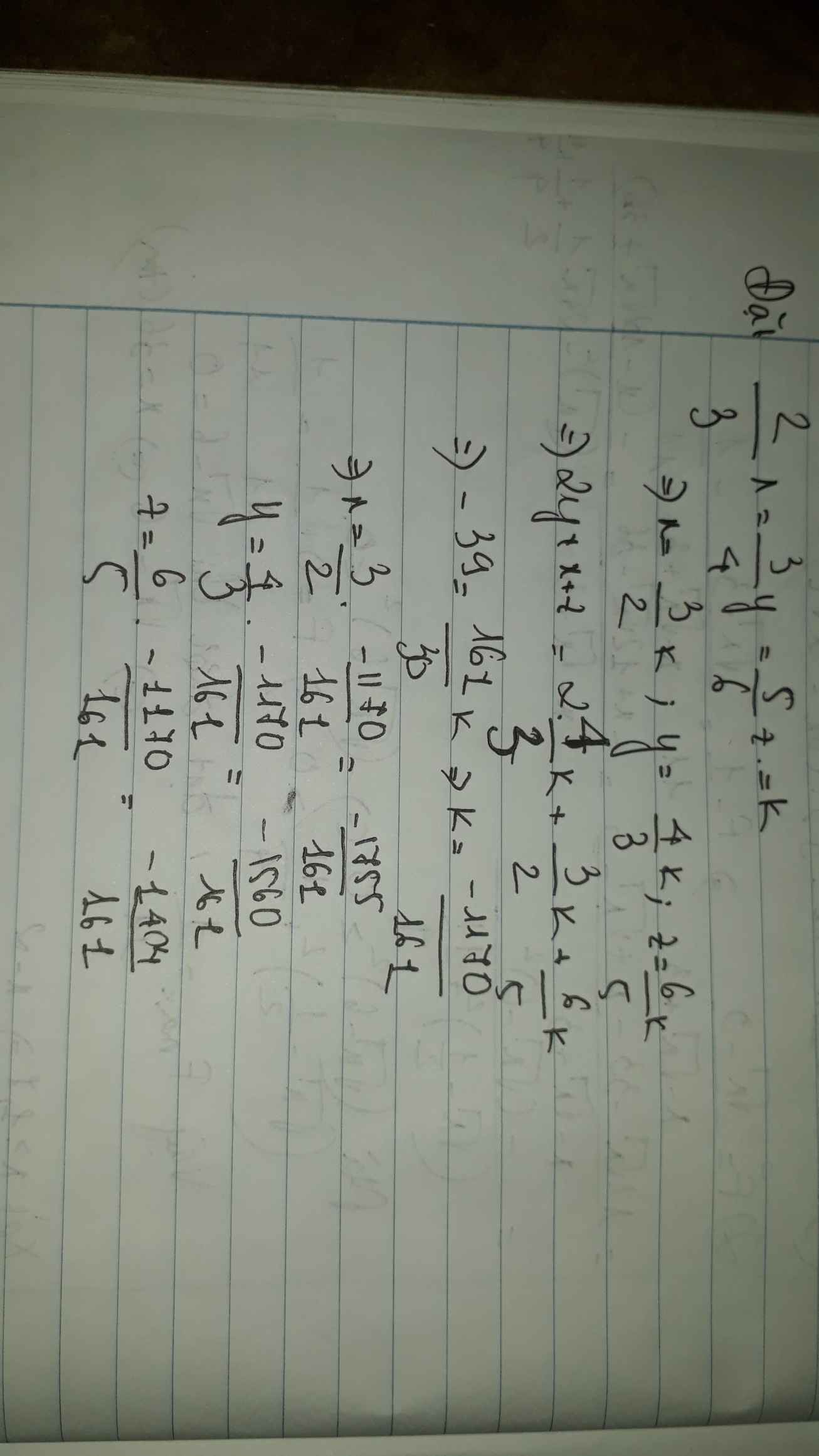
\(\dfrac{3x}{2}=\dfrac{4y}{3}=\dfrac{6z}{5}\Rightarrow\dfrac{x}{\dfrac{2}{3}}=\dfrac{y}{\dfrac{3}{4}}=\dfrac{z}{\dfrac{5}{6}}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{\dfrac{2}{3}}=\dfrac{y}{\dfrac{3}{4}}=\dfrac{z}{\dfrac{5}{6}}=\dfrac{x+y-z}{\dfrac{2}{3}+\dfrac{3}{4}-\dfrac{5}{6}}=\dfrac{-21}{\dfrac{7}{12}}=-36\\ \Rightarrow\left\{{}\begin{matrix}x=-36\cdot\dfrac{2}{3}=-24\\y=-36\cdot\dfrac{3}{4}=-27\\z=-36\cdot\dfrac{5}{6}=-30\end{matrix}\right.\)