Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

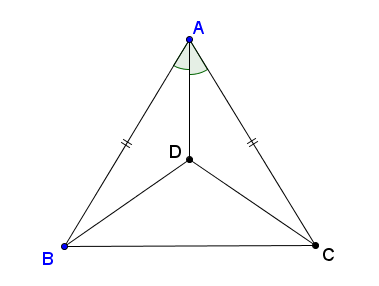
a) Căn cứ các kí hiệu đã cho trên hình của bài 39 ta có: ∆ABD và ∆ACD có:
AB = AC
ˆBAD=ˆCADBAD^=CAD^
AD là cạnh chung
=> ∆ABD = ∆ACD
b) Vì ∆ABD = ∆ACD
=> BD = CD => ∆BCD cân tại D
=> ˆDBC=ˆDCB
Hướng dẫn:
a) ∆KIL có ˆII^ = 620
nên ˆIKL+ˆILKIKL^+ILK^ = 1180
Vì KO và LO là phân giác ˆIKLIKL^, ˆILKILK^
nên ˆOKL+ˆOLKOKL^+OLK^= 1212(ˆIKL+ˆILKIKL^+ILK^)
=> ˆOKL+ˆOLKOKL^+OLK^ = 1212 1180
ˆOKL+ˆOLKOKL^+OLK^ = 590
∆KOL có ˆOKL+ˆOLKOKL^+OLK^ = 590
nên ˆKOLKOL^ = 1800 – 590 = 1210

c) Vì O là giao điểm của hai đường phân giác của ˆKK^ và ˆLL^ nên O cách đều ba cạnh của tam giác IKL

Vì ΔABD = ΔACD (chứng minh câu a)
⇒ BD = CD (hai cạnh tương ứng)
⇒ ΔBCD cân tại D
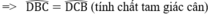

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Ta có: ΔADE cân tại A
mà AM là đường cao
nên AM là tia phân giác của góc DAE(đpcm)
c: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{BAH}=\widehat{CAK}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK; AH=AK
d: Xét ΔADE có
AH/AD=AK/AE
nên HK//DE

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Ta có: ΔADE cân tại A
mà AM là đường cao
nên AM là đường phân giác
hay \(\widehat{DAM}=\widehat{EAM}\)
c: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{BAH}=\widehat{CAK}\)
Do đó: ΔAHB=ΔAKC
Suy ra: BH=CK và AH=AK
d: XétΔADE có
AH/AD=AK/AE
nên HK//DE

Hình thiếu dữ kiện nên vẽ lại nhé!!
B C A D M
Gọi M là giao điểm của BC và AD
Xét tam giác ABM và tam giác DBM có:
AM = MD (GT)
\(\widehat{AMB}=\widehat{DMB}\)=900
BM: cạnh chung
=> tam giác ABM = tam giác DBM (c.g.c)
=> \(\widehat{ABM}=\widehat{DBM}\) (2 góc tương ứng)
=> BM hay BC là phân giác góc ABD (đpcm)
Xét tam giác ACM và tam giác DCM có:
AM = MD (GT)
\(\widehat{AMC}=\widehat{DMC}\)=900
CM: cạnh chung
=> tam giác ACM = tam giác DCM (c.g.c)
=> \(\widehat{ACM}=\widehat{DCM}\) (2 góc tương ứng)
=> CM hay CB là phân giác góc ACD (đpcm)

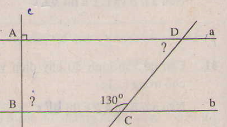

 Cho hình vẽ
Cho hình vẽ
Giải:
a, Xét \(\Delta ABD,\Delta ACD\) có:
\(AB=AC\left(gt\right)\)
\(\widehat{BAD}=\widehat{CAD}\left(gt\right)\)
AD: cạnh chung
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{ACD}\) ( góc t/ứng ) ( đpcm )
b, Ta có: AB = AC nên t/g ABC cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Mà \(\widehat{ABD}=\widehat{ACD}\)
\(\Rightarrow\widehat{ABC}-\widehat{ABD}=\widehat{ACB}-\widehat{ACD}\)
\(\Rightarrow\widehat{DBC}=\widehat{DCB}\) ( đpcm )
Vậy...
mình cảm ơn bạn nhiều