Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Lấy hai điểm A(0;4) và B(2;0) thuộc d. Gọi A′, B′ theo thứ tự là ảnh của A và B qua phép vị tự tâm O tỉ số k = 3. Khi đó ta có
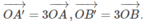
Vì O A → = ( 0 ; 4 ) nên O A ' → = ( 0 ; 12 ) . Do đó A′ = (0;12).
Tương tự B′ = (6;0); d1 chính là đường thẳng A'B' nên nó có phương trình:
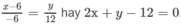
b) Có thể giải tương tự như câu a) .
Sau đây ta sẽ giải bằng cách khác.
Vì d 2 / / d nên phương trình của d 2 có dạng 2x + y + C = 0.
Gọi A′ = (x′;y′) là ảnh của A qua phép vị tự đó thì ta có:
I A ' → = − 2 I A → hay x′ + 1 = −2, y′ − 2 = −4
Suy ra x′ = −3, y′ = −2
Do A' thuộc d 2 nên 2.(−3) – 2 + C = 0.
Từ đó suy ra C = 8
Phương trình của d 2 là 2x + y + 8 = 0

Gọi \(M\left(x;y\right)\) là điểm bất kì thuộc d \(\Rightarrow3x-2y+3=0\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép vị tự nói trên \(\Rightarrow M'\in d'\) với d' là ảnh của d
Ta có:
\(\left\{{}\begin{matrix}x'=2x\\y'=2y\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}x'\\y=\dfrac{1}{2}y'\end{matrix}\right.\)
Thế vào (1):
\(\dfrac{3}{2}x'-y'+3=0\Leftrightarrow3x'-2y'+6=0\)
Vậy pt ảnh của d có dạng: \(3x-2y+6=0\)
https://hoc24.vn/cau-hoi/cau-1-cho-tam-giac-abc-can-tai-a-goi-cac-diem-pqm-lan-luot-la-trung-diem-cua-abacbc1chung-minh-tu-giac-pqcm-la-hinh-binh-hanh2tren-tia-doi.331415912641
Bác giúp e với ạ :))

Lời giải:
Xét $A(x,y)\in d$ và $M'(x',y')=T_{\overrightarrow{v}}$. Ta có:
\(\left\{\begin{matrix} x'-x=-2\\ y'-y=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x=x'+2\\ y=y'-5\end{matrix}\right.\)
Thay vào $(d)$:
$x'+2+y'-5+3=0$
$\Leftrightarrow x'+y'=0$ (đây là ptđt $d'$ cần tìm)


