Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt:
d=25cm
Vì là ảnh thật => k <0 =-2
f=?
Giải
Có k=-d'/d
<=> -2 =-d'/25
=> d'= 50cm
f= d.d'/d+d' = 25*50/25+50=50/3 cm
Thấu kính này là thấu kính hội tụ
bạn có f =50/3cm, d=25cm, d'=50cm rồi bạn căn vở rồi vẽ thôi nhé
Câu 2: Tóm tắt
d=30cm
Giải
Cho 2 trường hợp
Trường hợp một k = 1/2 >0 là ảnh ảo
k=-d'/d
<=> 1/2 = -d'/30
=> d' = -15cm
f=d.d'/d+d' = 30*(-15)/30-15= -30 (Vô lý vì k >0 là ảnh ảo thì f <0, d<0)
Trường hợp 2
k=-1/2 là ảnh thật
k=-d'/d
<=> -1/2 = -d'/30
=> d' =15
f=d.d'/d+d' = 30*15/30+ 15= 10 ( hợp lí vì k<0 là ảnh thật và f>0, d>0)
Từ đó suy ra trường hợp 2 đúng và kết luận đây là thấu kính hội tụ
Vẽ hình bạn chỉ cần cho vật lớn hơn 2f là được (d>2f)

Đáp án cần chọn là: C
Vật thật nên d > 0 ; ảnh ảo nên d ’ < 0 .
Áp dụng công thức thấu kính ta có:
1 d + 1 d ' = 1 f = 1 30 (1)
Khoảng cách giữa ảnh và vật là:
L = d + d ' = 40 c m ⇒ d + d ' = 40 d + d ' = − 40 (2)
Từ (1) và (2) ta có hệ phương trình:
d . d ' d + d ' = f ⇒ d . d ' 40 = 30 ( v o n g h i e m ) d . d ' − 40 = 30 ⇔ d = 20 c m d ' = 60 c m
Vậy khoảng cách từ vật đến TK gần nhất với 21 c m .

Đáp án cần chọn là: D
Ta có, vật AB qua thấu kính hội tụ cho ảnh ảo

Do ảnh thu được là ảnh ảo, nên ta có:
1 f = 1 d − 1 d ' (1)
Theo đầu bài, ta có: f = 30 c m d ' − d = 40 c m
Thay vào (1), ta được:
1 30 = 1 d − 1 d + 40
↔ d d + 40 = 30 d + 40 − 30 d
↔ d 2 + 40 d − 1200 = 0
→ d = 20 c m d = − 60 c m

Chọn đáp án A
Thấu kính vừa cho ảnh thật, vừa cho ảnh ảo => thấu kính hội tụ.
d 1 = 16 c m ; d ' > 0 d > 2 0 ; d ' ' = − 24 c m k 1 = − k 2
⇔ − d ' ' d 2 = d ' d 1 ⇒ d ' . d 2 = − d 1 d ' ' = 384. ⇒ d ' = 384 d 2 ( 1 )
* f = d 1 d ' d 1 + d ' = d 2 d ' ' d 2 + d ' ' ⇔ 16 d ' 16 + d ' = − 24 d 2 d 2 − 24 ( 2 )
( 1 ) , ( 2 ) ⇒ d ' = 48 ( c m ) ⇒ f = 12 ( c m ) .

Sơ đồ tạo ảnh
![]() a) Ta có:
d
1
'
=
d
1
f
1
d
1
-
f
1
=
120
c
m
;
a) Ta có:
d
1
'
=
d
1
f
1
d
1
-
f
1
=
120
c
m
;
d 2 = O 1 O 2 - d 1 ' = l - d 1 ' = - 90 c m ; d 2 ' = d 2 f 2 d 2 - f 2 = - 180 7 c m ;
k = A 2 B 2 A B = A 1 B 1 A B . A 2 B 2 A 1 B 1 = - d 1 ' d 1 . - d 2 ' d 2 = d 1 ' d 2 ' d 1 d 2 = 120 . - 180 7 60 . ( - 90 ) = 4 7 .
Vậy: Ảnh cuối cùng là ảnh ảo ( d 2 ' < 0 ); cùng chiều với vật (k > 0) và nhỏ hơn vật (|k| < 1).
b) Ta có: d 1 ' = d 1 f 1 d 1 - f 1 = 40 d 1 d 1 - 40 ; d 2 = l - d 1 ' = - 10 d 1 + 1200 d 1 - 40 ;
d 2 ' = d 2 f 2 d 2 - f 2 = 20 d 1 + 2400 d 1 - 200
Để ảnh cuối cùng là ảnh thật thì d 2 ' > 0 ⇒ d2 > 200 cm.
c) Ta có: d 1 ' = d 1 f 1 d 1 - f 1 = 120 c m ; d 2 = l - d 1 ' = l - 120 ;
d 2 ' = d 2 f 2 d 2 - f 2 = - 20 ( l - 200 ) l - 100 ; k = d 1 ' d 2 ' d 1 d 2 = 40 100 - l .
Để ảnh cuối cùng là ảnh thật thì d 2 ' > 0 ⇒ 120 > l > 100; để ảnh cuối cùng lớn gấp 10 lần vật thi k = ± 10 ⇒ l = 96 cm hoặc l = 104 cm. Kết hợp cả hai điều kiện ta thấy để ảnh cuối cùng là ảnh thật lớn gấp 10 lần vật thì l = 104 cm và khi đó ảnh ngược chiều với vật

Sơ đồ tạo ảnh:
![]()
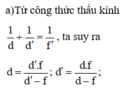
Số phóng đại ảnh qua thấu kính: k = − d ' d
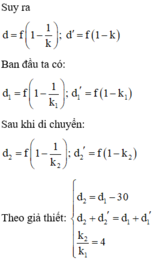
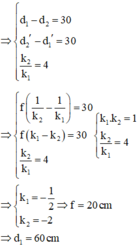
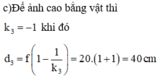
Như vậy để có ảnh cao bằng vật thì cần dịch chuyển vật lại gần thấu kính một đoạn 60 - 40 = 20 cm

Đáp án cần chọn là: C
Tiêu cự của kính: f = 30 c m
Công thức thấu kính: 1 d + 1 d ' = 1 f
Ảnh của vật tạo bởi thấu kính là ảnh ảo và cách vật là 40cm. Ta có:
d + d ' = 40 c m ⇒ d + d ' = 40 c m d + d ' = − 40 c m
TH1: d + d ' = 40 c m ⇒ d ' = 40 − d
Thay vào công thức thấu kính ta có:
1 d + 1 40 − d = 1 30 ⇒ d = − 30 c m l o a i
TH2: d + d ' = − 40 c m ⇒ d ' = − 40 − d
Thay vào công thức thấu kính ta có:
1 d − 1 40 + d = 1 30 ⇒ d = 20 c m t / m
Khoảng cách từ AB đến thấu kính có giá trị gần nhất với giá trị 26cm.

18Chọn đáp án D.
Gọi khoảng cách từ vật tới thấu kính là d (cm). Ta có:
Vì ảnh ảo cách vật 40 cm nên d ’ < 0 → d + d ’ = - 40 ( c m )
1 f = 1 d + 1 d ' ⇔ 1 30 = 1 d + 1 − d − 40 ⇒ d = 20 c m .
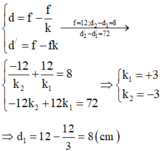
3/ \(n\sin i=\sin60^0;\) \(i=90-r\Rightarrow i=30^0\)
\(\Rightarrow n=\dfrac{\sin60^0}{\sin30^0}=\sqrt{3}\)
5/ \(D=\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow2=\dfrac{1}{0,25}+\dfrac{1}{d'}\Rightarrow d'=-50\left(cm\right)\)
\(k=-\dfrac{d'}{d}=\dfrac{50}{25}=2\)
=>D. Anh ao, cach thau kinh 50cm, k=2
7/ \(d=\dfrac{d'f}{d'-f}\Rightarrow d+d'=d'+\dfrac{d'f}{d'-f}=\dfrac{d'^2-d'f+d'f}{d'-f}=\dfrac{d'^2}{d'-f}\)
\(\left(d+d'\right)_{min}\Leftrightarrow(\dfrac{1}{d'}-\dfrac{f}{d'^2})_{max}\)
Dat \(\dfrac{1}{d'}=a\Rightarrow a-a^2f=-\left(a^2f+a+\dfrac{1}{4f}\right)+\dfrac{1}{4f}=-\left(a\sqrt{f}+\dfrac{1}{2\sqrt{f}}\right)^2\le\dfrac{1}{4f}\)
\("="\Leftrightarrow a\sqrt{f}=\dfrac{1}{2\sqrt{f}}\Leftrightarrow2af=1\Rightarrow a=\dfrac{1}{2f}\)
\(\Rightarrow\dfrac{1}{d'}=\dfrac{1}{2f}\Rightarrow d'=2f\Rightarrow d=\dfrac{d'f}{d'-f}=\dfrac{2f^2}{2f-f}=2f\)
\(\Rightarrow\left(d+d'\right)_{min}=2f+2f=4f\Rightarrow D.4f\)
8/ \(D=\dfrac{1}{f}=-\dfrac{1}{20}=-0,05\left(dp\right)\Rightarrow C.-0,05dp\)
15/ \(k_1=\dfrac{f}{f-d_1};k_2=\dfrac{f}{f-d_2};\dfrac{k_1}{k_2}=-1\)
\(d_2=d_1-12\Rightarrow\dfrac{k_1}{k_2}=-1=\dfrac{f-d_2}{f-d_1}=\dfrac{f-d_1-12}{f-d_1}\) (1)
\(\dfrac{1}{f}=\dfrac{1}{d_1}+\dfrac{1}{d_1'};-\dfrac{d'_1}{d_1}=3\Rightarrow\dfrac{1}{f}=\dfrac{1}{d_1}-\dfrac{1}{3d_1}\)
\(\Rightarrow\dfrac{1}{f}=\dfrac{2}{3d_1}\Rightarrow d_1=\dfrac{2}{3}f\)
Thay vo (1)\(\Rightarrow\dfrac{f-\dfrac{2}{3}f-12}{f-\dfrac{2}{3}f}=-1\Leftrightarrow\dfrac{1}{3}f-12=-\dfrac{1}{3}f\Rightarrow f=18\left(cm\right)\)
19/ \(\sin i=n\sin r=n\cos i\Rightarrow\tan i=n\Rightarrow A.\tan i=n\)
22/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow\dfrac{1}{20}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(-d'-d=45\Rightarrow d'=-d-45\Rightarrow\dfrac{1}{20}=\dfrac{1}{d}-\dfrac{1}{d+45}\)
\(\Leftrightarrow d^2+45d=45.20\Leftrightarrow\left[{}\begin{matrix}d=15\left(cm\right)\\d=-60\left(loai\right)\end{matrix}\right.\Rightarrow d'=-60\left(cm\right)\)