
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x\left(3x-4\right)=2x^2+1\)
\(\Leftrightarrow3x^2-4x-2x^2-1=0\)
\(\Leftrightarrow x^2-4x-1=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=4\\x_1x_2=\dfrac{c}{a}=-1\end{matrix}\right.\)
Ta có :
\(A=x_1^2+x_2^2+3x_1x_2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2+3x_1x_2\)
\(=\left(x_1+x_2\right)^2+x_1x_2\)
\(=4^2-1\)
\(=16-1\)
\(=15\)

a) Ta có: \(x^2-11x-26=0\)
nên a=1; b=-11; c=-26
Áp dụng hệ thức Viet, ta được:
\(x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-11\right)}{1}=11\)
và \(x_1x_2=\dfrac{c}{a}=\dfrac{-26}{1}=-26\)

2x2-5x + 2m - 1 = 0 ( 1)
Dental = (-5)2 - 4*2*( 2m - 1)
= 25 - 16m + 8
= 33 - 16m
Phương trình (1) có 2 nghiệm phân biệt khi :
33 - 16m > 0
- 16m >-33
m < 33/16
Theo hệ thức vi-ét ta có:
x1 + x2 = -b/a = 5/2
x1x2 = c/a =2m - 1/2
Theo bài ch0 :1/x1 + 1/x2 = 5/2
<=>2( x2 + x1 ) = 5x1x2
<+> 2( 5/2 ) + 55 ( 2m - 1 ?2
<+> 5 = 10m -5?2
<+>
<=>2( x2 + x1 ) = 5x1x2
<=> 2( 5/2 ) = 5 ( 2m - 1 /2 )
<=> 5 - 10m + 5/2 = 0
<=> 10 - 20m + 5 = 0
<=> 15 - 20m = 0
<=> -20m = -15
<=> m = 5/4
Vậy m = 5/4 thỏa mãn yêu cầu bài toán
( mình học khá nên chắc không đúng 100 %, có sai xót thì mng sửa hộ ạ ^^ )

a) Thay m=2 vào phương trình \(x^2+2\left(m-1\right)x-4m=0\), ta được:
\(x^2+2\cdot\left(2-1\right)x-4\cdot2=0\)
\(\Leftrightarrow x^2+2x-8=0\)(1)
\(\Delta=b^2-4ac=2^2-4\cdot1\cdot\left(-8\right)=4+32=36\)
Vì \(\Delta>0\) nên phương trình (1) có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-b-\sqrt{\Delta}}{2a}\\x_2=\dfrac{-b+\sqrt{\Delta}}{2a}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-2-\sqrt{36}}{2\cdot1}=\dfrac{-2-6}{2}=-4\\x_2=\dfrac{-2+\sqrt{36}}{2\cdot1}=\dfrac{-2+6}{2}=2\end{matrix}\right.\)
Vậy: Khi m=2 thì phương trình \(x^2+2\left(m-1\right)x-4m=0\) có hai nghiệm phân biệt là \(x_1=-4;x_2=2\)
b) Ta có: \(x^2+2\left(m-1\right)x-4m=0\)
\(\Delta=\left[2\left(m-1\right)\right]^2-4\cdot1\cdot\left(-4\right)\)
\(\Leftrightarrow\Delta=\left(2m-2\right)^2+16>0\forall m\)
\(\forall m\) thì phương trình \(x^2+2\left(m-1\right)x-4m=0\) luôn có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-\left(2m-2\right)-\sqrt{\Delta}}{2}\\x_2=\dfrac{-\left(2m-2\right)+\sqrt{\Delta}}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-2m+2-\sqrt{\left(2m-2\right)^2+16}}{2}\\x_2=\dfrac{-2m+2+\sqrt{\left(2m-2\right)^2+16}}{2}\end{matrix}\right.\)
Để x1 và x2 là hai số đối nhau thì \(x_1+x_2=0\)
\(\Leftrightarrow\dfrac{-2m+2-\sqrt{\left(2m-2\right)^2+16}}{2}+\dfrac{-2m+2+\sqrt{\left(2m-2\right)^2+16}}{2}=0\)
\(\Leftrightarrow-2m+2-2m+2=0\)
\(\Leftrightarrow-4m+4=0\)
\(\Leftrightarrow-4m=-4\)
hay m=1
Vậy: Khi m=1 thì phương trình \(x^2+2\left(m-1\right)x-4m=0\) có hai nghiệm phân biệt x1 và x2 thỏa mãn x1 và x2 là hai số đối nhau
a, Với m = 2 (1)<=>x^2+2x-8=0 rồi tính ra thôi
b, Để PT có 2 nghiệm PB thì
Δ=[2(m−1)]^2−4⋅1⋅(−4)Δ=[2(m−1)]2−4⋅1⋅(−4)
⇔Δ=(2m−2)^2+16>0∀m
Vì x1 và x2 là 2 số đối nhau nên x1+x2=0 <=> -2(m-1) = 0 <=> m=1
Vậy để PT có 2 nghiệm pbiet đối nhau thì m = 1

\(2x^2-6x-3=0\)
\(\Delta'=3^2+3.2=15>0\)
⇒ Phương trình có hai nghiệm phân biệt.
Theo hệ thức viét có : \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=-\dfrac{3}{2}\end{matrix}\right.\)
Ta có : \(A=x_1^2x_2^2-2x_1-2x_2=\left(x_1x_2\right)^2-2\left(x_1+x_2\right)=\left(-\dfrac{3}{2}\right)^2-2.3=-\dfrac{15}{4}\)
Vậy \(A=-\dfrac{15}{4}\) thì thỏa mãn điều kiện bài ra.

Ta có: \(\Delta'=32>0\)
\(\Rightarrow\) Phương trình có 2 nghiệm phân biệt
Theo Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=12\\x_1x_2=4\end{matrix}\right.\)
Mặt khác: \(T=\dfrac{x_1^2+x^2_2}{\sqrt{x_1}+\sqrt{x_2}}\)
\(\Rightarrow T^2=\dfrac{x_1^4+x^4_2+2x_1^2x_2^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(x_1^2+x_1^2\right)^2}{x_1+x_2+2\sqrt{x_1x_2}}\) \(=\dfrac{\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2}{x_1+x_2+2\sqrt{x_1x_2}}=\dfrac{\left(12^2-2\cdot4\right)^2}{12+2\sqrt{4}}=1156\)
Mà ta thấy \(T>0\) \(\Rightarrow T=\sqrt{1156}=34\)

Theo định lý Vi-et ta có: phương trình
a
x
2
+
b
x
+
c
= 0 có hai nghiệm
x
1
;
x
2
thì: 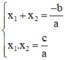
Ta sử dụng một trong hai biểu thức trên để tìm nghiệm còn lại.
Ở bài giải dưới đây ta sẽ sử dụng điều kiện: 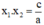
(Các bạn có thể làm cách 2 sử dụng điều kiện 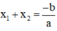 ).
).
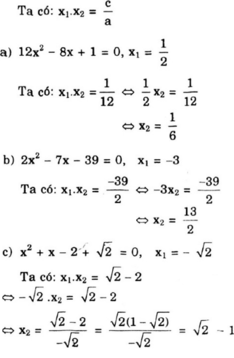
d) x 2 - 2 m x + m - 1 = 0 ( 1 )
Vì x 1 = 2 là một nghiệm của pt (1) nên:
2 2 - 2 m . 2 + m - 1 = 0
⇔ 4- 4 m+ m – 1 = 0
⇔ 3- 3m = 0
⇔ m = 1
Khi m = 1 ta có: x 1 . x 2 = m - 1 (hệ thức Vi-ét)
⇔ 2 . x 2 = 0 ( v ì x 1 = 2 và m = 1)
⇔ x 2 = 0
\(2x^2-6x-1=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{6}{2}=3\\x_1x_2=\dfrac{c}{a}=-\dfrac{1}{2}\end{matrix}\right.\)
Ta có :
\(A=\dfrac{x_1-2}{x_2-1}+\dfrac{x_2-2}{x_1-1}\)
\(=\dfrac{\left(x_1-2\right)\left(x_1-1\right)+\left(x_2-2\right)\left(x_2-1\right)}{\left(x_2-1\right)\left(x_1-1\right)}\)
\(=\dfrac{x_1^2-x_1-2x_1+2+x_2^2-x_2-2x_2+2}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2-3\left(x_1+x_2\right)+4}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3^2-2.\left(-\dfrac{1}{2}\right)-3.3+4}{-\dfrac{1}{2}-3+1}\)
\(=-2\)