Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Độ dài chiều cao là:
5,6 : 20% = 28 (m)
Tổng độ dài 2 đáy là:
28 x 120% = 33,6 (m)
Diện tích hình thang là:
33,6 x 28 : 2 = 470,4 (m2m2 )
Đáp số: 470,4m2
Bài 18:
Theo định lý Pitago:
\(SA=\sqrt{SB^2-AB^2}=2a\)
Do đó, \(V_{S.ABC}=\frac{1}{3}.SA.S_{ABC}=\frac{1}{3}.2a.\frac{a.5a}{2}=\frac{5a^3}{3}\)
Đáp án D.
Bài 19:
Vì
\(SA\perp (ABCD)\Rightarrow \angle (SB,(ABCD))=\angle (SB,AB)=\angle SBA=60^0\)
Suy ra \(\frac{SA}{AB}=\frac{SA}{a}=\tan SBA=\sqrt{3}\Rightarrow SA=\sqrt{3}a\)
\(\Rightarrow V_{S.ABCD}=\frac{1}{3}.SA.S_{ABCD}=\frac{1}{3}\sqrt{3}a.a.3a=\sqrt{3}a^3\)
Đáp án B
giup minh voi
ý a,b,c cho 2 tung độ bằng nhau => tính được x1, x2 rồi áp dụng CT diện tích như thường
ý d cũng vậy => tính được x1, x2 nhưng phải xét điều kiện của e^x (x>0)
ý e :
ta có y' = 2x-2 mà M thuộc y' => y' = 4
=> PTTT là: y= 4x-7
xét x^2-2x+2 = 4x-7
=> tính được x1, x2 rồi áp dụng công thức diện tích như 4 ý trên
TXĐ: D=R, y'=-x2+10x-26=0 < 0 với mọi x.
Vậy hàm số đã cho nghịch biến trên khoảng (-\(\infty\);+\(\infty\)).
Lời giải:
Ta có \(y'=1-m\sin x\). Để hàm số nghịch biến trên R thì \(y'\leq 0\) với mọi \(x\in\mathbb{R}\)
\(\Leftrightarrow 1-m\sin x\leq 0\Leftrightarrow m\sin x\geq 1\)
Nếu \(\sin x=0\) thì hiển nhiên \(m\sin x<1\) nên không tìm được m hợp lý
Nếu đề bài là đồng biến trên R thì bài toán sẽ được giải quyết.
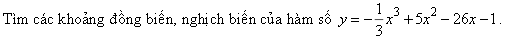
mấy chữ k là j vậy
ko có đề à?