Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai tam giác đồng dạng chưa chắc sẽ bằng nhau còn khi 2 tam giác bằng nhau thì chắc chắn chúng sẽ đồng dạng. giải thích : Hai Δ có ti số đồng dạng là 1/2 hay 1/3 thì sẽ không bằng nhau tại vì 2 tam giác bằng nhau sẽ có tỉ lệ là 1:1
Hai tam giác đồng dạng với nhau nếu một trong hai cặp góc và một cặp cạnh tương ứng bằng nhau. ... Vì vậy, nếu hai tam giác bằng nhau, thì cạnh và góc bên thứ ba cũng bằng nhau
Hai tam giác đồng dạng với nhau nếu một trong hai cặp góc và một cặp cạnh tương ứng bằng nhau. Cơ sở của lý thuyết này là tính chất tổng 3 góc trong tam giác. Theo tính chất tổng góc, tổng ba góc trong một tam giác là 180°. Vì vậy, nếu hai tam giác bằng nhau, thì cạnh và góc bên thứ ba cũng bằng nhau

a) Ta có:
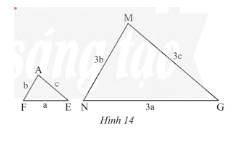
\(\frac{{AF}}{{MN}} = \frac{b}{{3b}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{c}{{3c}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{a}{{3a}} = \frac{1}{3}\)
Xét tam giác \(AFE\) và tam giác \(MNG\) có:
\(\frac{{AF}}{{MN}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{1}{3} \Rightarrow \frac{{AF}}{{MN}} = \frac{{AE}}{{MG}} = \frac{{EF}}{{NG}}\)
Do đó, \(\Delta AFE\backsim\Delta MNG\) (c.c.c)
b) Tỉ số đồng dạng của tam giác \(AFE\) và tam giác \(MNG\) là \(\frac{1}{3}\).
Do đó, tỉ số chu vi của của tam giác \(AFE\) và tam giác \(MNG\) là \(\frac{1}{3}\) (tính chất)
Do đó, chu vi tam giác \(MNG\) là: \(15.3 = 45cm\)
Vậy chu vi tam giác \(MNG\) là 45 cm.

Bạn ơi 2 tam giác đồng dạng có 2 cặp cạnh bằng nhau thì chưa chắc đã bằng nhau nhé! Phải là tỉ số giữa 2 cặp cạnh t/ứng và 1 cặp góc t/ứng thì mới bằng nhau được. Đây là một số kiến thức quan trọng cần nhớ nè:
- 2 tam giác bằng nhau thì chắc chắn đồng dạng
- 2 tam giác đồng dạng chưa chắc đã bằng nhau
- Tam giác đồng dạng với nhau dựa vào tỉ số giữa các đoạn thẳng và góc.
- Tam giác đồng dạng bằng nhau cũng có 3 trường hợp giống tam giác thường và tam giác vuông:
+) C.c.c: tỉ số bằng nhau giữa 3 cặp cạnh t/ứng
+) G.g: tỉ số bằng nhau giữa 2 cặp góc t/ứng
+) C.g.c: tỉ số bằng nhau giữa 2 cặp cạnh t/ứng và 1 cặp góc t/ứng
Nếu bạn chưa hiểu thì inbox với mình, mình sẽ giảng cụ thể hơn. Chúc bạn học tốt!!!

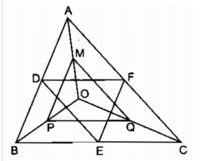
Theo giả thiết D, E, F lần lượt là trung điểm các cạnh AB, BC và CA nên DE, EF, FD là các đường trung bình của tam giác ABC. Do đó, ta có:
DE = 1/2 AC,EF = 1/2 AB,FD = 1/2 BC (1)
Mặt khác, M là trung điểm của OA, P là trung điểm của OB, Q là trung điểm của OC, xét các tam giác OAB, OBC, OCA, ta cũng có:
MP = 1/2 AB,PQ = 1/2 BC, QM = 1/2 AC. (2)
Từ đẳng thức (1) và (2), ta suy ra :
DE = QM, EF = MP, FD = PQ.
Do đó ta có: 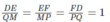
Vậy △ DEF đồng dạng △ QMP theo tỉ số đồng dạng k = 1, trong đó D, E, F lần lượt tương ứng với các đỉnh Q, M, P.

* Trong tam giác vuông A’B’C’ có ∠ A ' = 90 0
Áp dụng định lí Pi-ta-go, ta có: A ' B ' 2 + A ' C ' 2 = B ' C ' 2
Suy ra: A ' C ' 2 = B ' C ' 2 - A ' B ' 2 = 15 2 - 9 2 = 144
Suy ra: A’C’ = 12 (cm)
* Trong tam giác vuông ABC có ∠ A = 90 0
Áp dụng định lí Pi-ta-go, ta có: B C 2 = A B 2 + A C 2 = 6 2 + 8 2 =100
Suy ra: BC = 10 (cm)
Ta có: 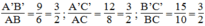
Suy ra: 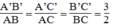
Vậy △ A’B’C’ đồng dạng ΔABC (c.c.c)

Hai tam giác bằng nhau là hai tam giác đồng dạng với tỉ số đồng dạng là k = 1 nhưng chưa hẳn là hai hình đồng dạng phối cảnh vì khi nối các đỉnh tương ứng thì chưa chắc chúng đồng quy tại một điểm


Hai tam giác bằng nhau thì đồng dạng
Hai tam giác đồng dạng thì chưa chắc bằng nhau
Vì sao ạ bạn