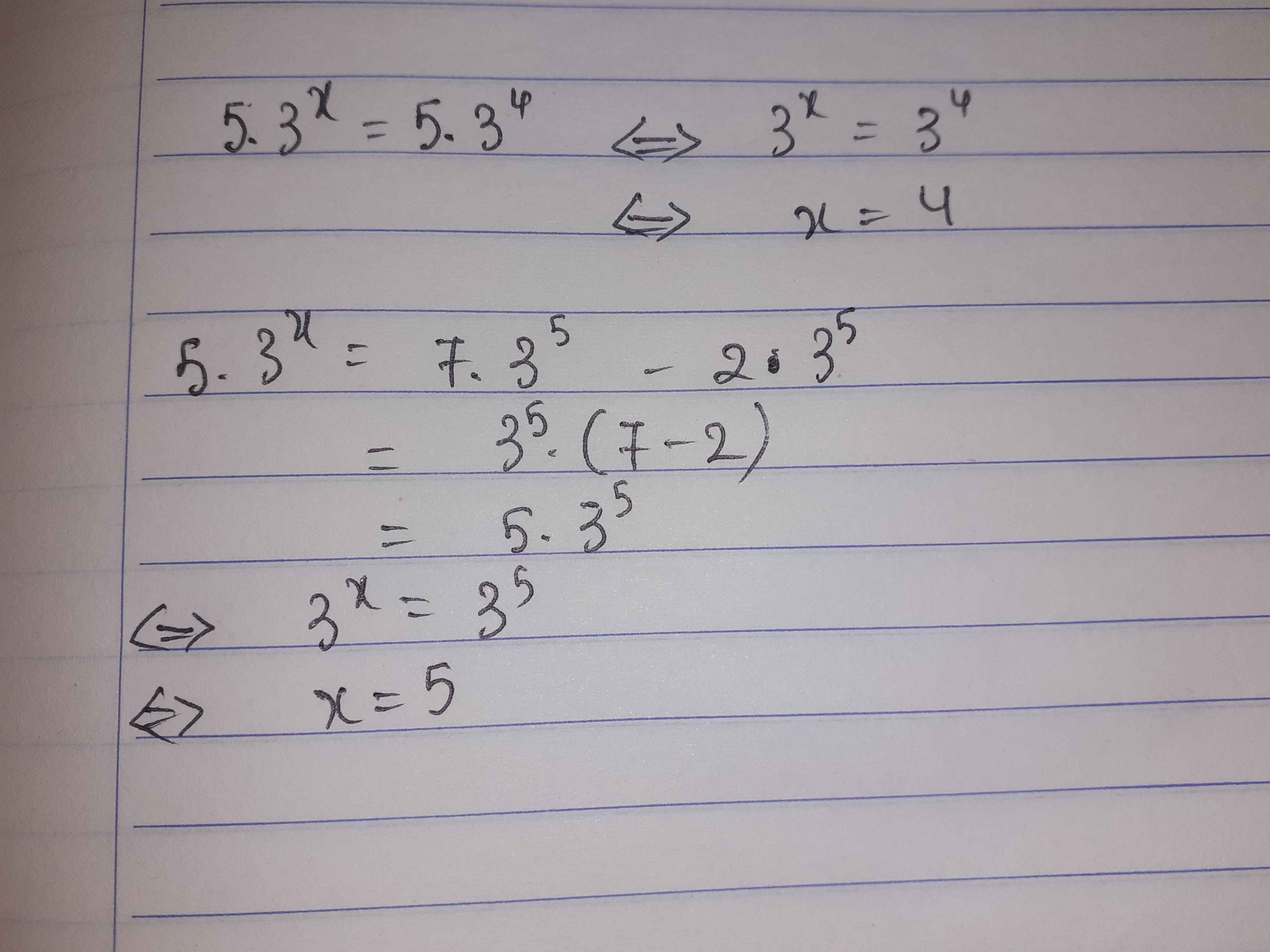PA
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
4
12 tháng 7 2021
5.3x = 5.34
=> x = 4
5.34 = 7.35 - 2.35
= 35 . (7 - 2)
= 5. 35
=> 3x = 35
=> x = 5
NN
16 tháng 2 2017
\(a,\frac{5\cdot6+5\cdot7}{5\cdot8+20}=\frac{\left(5\cdot6+5\cdot7\right)\div2}{\left(5.8+20\right)\div2}=\frac{13}{12}\)
\(\frac{8.9-4.15}{12.7-180}=\frac{12.6-12.5}{12.7-12.15}=\frac{1}{-8}=\frac{-1}{8}\)
\(Ta\)\(co\)\(\frac{13}{12}=\frac{13.2}{12.2}=\frac{26}{24}\)
\(\frac{-1}{8}=\frac{3\left(-1\right)}{3.8}=\frac{-3}{24}\)
Phần b bạn tính ra rồi làm tương tự phần a nha chúc bạn học giỏi!!!
T
13 tháng 2 2018
1. Tìm x, biết:
a) \(\frac{4}{x}=\frac{8}{6}\). Ta có: \(\frac{8}{6}=\frac{8:2}{6:2}=\frac{4}{3}\Rightarrow x=3\)
b) \(\frac{3}{x-5}=\frac{4}{x+2}\). Ta có: \(5-2=3\)
\(\Rightarrow x=\left(3.5\right)+\left(4.2\right)+3=15+8+3=26\)
c) \(\frac{x}{-2}=\frac{-8}{x}\Rightarrow x=\left(-8\right):\left(-2\right)=4\)
2. Rút gọn
a) \(\frac{2^4.5^2.11^2.7}{2^3.5^3.7^2.11}\Leftrightarrow\frac{2^3.2^1.5^2.11.11.7}{2^3.5^2.5^1.7.7.11}\Leftrightarrow\frac{2^1.11}{5^1.7}=\frac{22}{35}\)
b) Tương tự
c) Tương tự
13 tháng 2 2018
\(\frac{4}{x}=\frac{8}{6}\Rightarrow x=\frac{4.6}{8}=3\)
\(\frac{3}{x-5}=\frac{-4}{x+2}\Rightarrow3\left(x+2\right)=-4\left(x-5\right)\)
\(\Rightarrow3x+6=-4x+20\)
\(\Rightarrow3x+4x=20-6\)
\(\Rightarrow7x=14\)
\(\Rightarrow x=2\)
\(\frac{x}{-2}=\frac{-8}{x}\Rightarrow x^2=\left(-8\right)\left(-2\right)=16\Rightarrow x=\pm4\)
IA
12 tháng 7 2021
c, \(5^{x+4}-3\cdot5^{x+3}=2\cdot5^{11}\)
\(\Leftrightarrow5^{x+3}\cdot5-3\cdot5^{x+3}=2\cdot5^{11}\)
\(\Leftrightarrow5^{x+3}\left(5-3\right)=2\cdot5^{11}\)
\(\Leftrightarrow5^{x+3}\cdot2=2\cdot5^{11}\)
\(\Leftrightarrow5^{x+3}=5^{11}\)
\(\Leftrightarrow x+3=11\)
\(\Leftrightarrow x=8\)
Vậy x = 8
d, \(2^x+2^{x+1}+2^{x+2}+2^{x+3}+2^{x+4}+2^{x+5}=480\)
\(\Leftrightarrow2^x\left(1+2+2^2+2^3+2^4+2^5\right)=480\)
\(\Leftrightarrow2^x\cdot63=480\)
\(\Leftrightarrow2^x=\frac{160}{21}\)
\(\Leftrightarrow x\approx2,93\)
8 tháng 2 2017
Ta có: \(\frac{2^5.7+2^5}{2^5.5^2-2^5.3}\) = \(\frac{2^5.\left(7+1\right)}{2^5.\left(5^2-3\right)}\) = \(\frac{2^5.8}{2^5.22}\) = \(\frac{8}{22}\) =\(\frac{56}{154}\)
\(\frac{3^4.5-3^6}{3^4.13+3^4}\) = \(\frac{3^4.\left(5-3^2\right)}{3^4.\left(13+1\right)}\) = \(\frac{3^4.\left(-4\right)}{3^4.14}\) = \(\frac{-4}{14}\)= \(\frac{-44}{154}\)