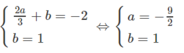Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=-1\\2a+b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=2\end{matrix}\right.\)

Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b+1=0\\2a+b+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=-1\\2a+b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=2\end{matrix}\right.\)

Theo đề, ta có:
\(\left\{{}\begin{matrix}a+b=-1\\4a+b=-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=0\end{matrix}\right.\)

Câu 1:
Đỉnh của đths \((\frac{-b}{2a}, \frac{4ac-b^2}{4a})=(\frac{-b}{4},\frac{8c-b^2}{8})=(-1;0)\)
\(\Leftrightarrow \left\{\begin{matrix} \frac{-b}{4}=-1\\ \frac{8c-b^2}{8}=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=4\\ 8c=b^2=16\end{matrix}\right.\Leftrightarrow b=4; c=2\)
Câu 2:
ĐTHS đi qua 3 điểm $A, B,C$ nên:
\(\left\{\begin{matrix}
-1=a.0^2+b.0+c\\
-1=a.1^2+b.1+c\\
1=a(-1)^2+b(-1)+c\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}
c=-1\\
a+b+c=-1\\
a-b+c=1\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} c=-1\\ a=1\\ b=-1\end{matrix}\right.\)

Với \(a\ne0\) từ đề bài ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=2\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}4a+b=0\\4a+2b+c=1\\16a+4b+c=-3\end{matrix}\right.\)
\(\Rightarrow a=-1;b=4;c=-3\)
Vậy (P): \(y=-x^2+4x-3\)

Vì đồ thị đi qua A(2/3; -2) nên ta có phương trình 2a/3 + b = -2
Tương tự, dựa vào tọa độ của B(0 ;1) ta có 0 + b = 1.
Vậy, ta có hệ phương trình.