Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath


a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

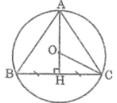
Vì O là tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Kẻ AH ⊥ BC. Ta có: O ∈ AH
Trong tam giác vuông ABH, ta có:
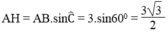
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
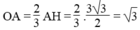
Vậy chọn đáp án C.

Đáp án là C
Tam giác ABC có:
A B 2 + A C 2 = 12 2 + 16 2 = 400 = B C 2
⇒ ΔABC vuông tại A
⇒ Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của BC
⇒ Bán kính = 10 cm

Đáp án là B
Xét tam giác ABC có:
A B 2 + A C 2 = 7 2 + 24 2 = 625 = B C 2
⇒ ΔABC vuông tại A
⇒ Tâm đường tròn ngoại tiếp tam giác ABC là trung điểm của cạnh huyền BC
⇒ Bán kính đường tròn ngoại tiếp là 12,5 cm


