Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)
Mình ra có 4 điểm thôi bạn ơi, xem hộ mình xem có nhầm lẫn ở đâu không nhé (mình tin là các bước làm là đúng rồi, sợ thay sai ở đâu đó thôi)
Gọi giao điểm của đường tròn với đoạn AB ll là D, E (bạn vẽ hình ra cho dễ nhìn nhé). để xác định số điểm theo đề ta chỉ cần xác định số điểm M nằm trên đoạn DE dao động với biên độ 8cm
Ta có: \(U_{am}=3cos\left(10\pi t-\frac{10\pi d_1}{50}\right)\)(d1:khoảng cách MA)
\(U_{bm}=5cos\left(10\pi t-\frac{10\pi\left(30-d_1\right)}{50}+\frac{\pi}{3}\right)=5cos\left(10\pi t+\frac{\pi}{5}d_1+\frac{\pi}{3}\right)\)
độ lệch pha giữa hai dao động thành phần: \(\Delta\varphi=\frac{2\pi}{5}d_1+\frac{\pi}{3}\left(1\right)\)
ta có biên độ dao động tại M (theo tổng hợp dao dộng, bạn vẽ giản đồ vectơ cho dễ nhìn): (một cách trực quan ta thấy luôn 8=3+5. do đó hai dao động thành phần phải cùng pha. tuy nhiên để ở đây mình làm theo công thức đơn thuần) \(8^2=5^2+3^2+2.5.3.cos\Delta\varphi\Rightarrow\Delta\varphi=2k\pi\left(2\right)\)
từ (1) và (2) và M thuộc DE ta được \(13\le d_1=5k-\frac{5}{6}\le23\Rightarrow3\le k\le4\)
=>có 2giá trị của k tương ứng với có 2 điểm M nằm trên đoạn DE không trùng với D, E dao động với biên độ 8cm (nói cách khác là thuộc khoảng DE) =>trên đường tròn đề bài ra có 2*2=4 điểm
Chọn D
Ta có sóng dừng với hai đầu cố định có 6 nút tính cả hai đầu AB nên trên sợi dây AB hình thành sóng dừng với số bụng là 5
l
=
5
λ
2
⇒
λ
=
10
c
m
A
M
=
1
c
m
<
λ
4
⇒
M nằm giữa nút A với điểm bụng C gần A nhất trong bó sóng đầu tiên
Ta có các phần tử cùng biên độ thì chúng đối xứng nhau qua một bụng hoặc qua một nút,các phần tử ở cùng một bụng dao dộng cùng pha,hai phần tử ở hai nút liền kề nhau cùng biên độ nhưng dao động ngược pha
như vậy trên AB có ba bó sóng mà ở đó các phần tử đao dộng cùng pha nhau
Một bóng sóng ta luôn tìm được hai điểm cùng biên độ đối xứng nhau qua bụng như vậy từ ba bó sóng đó ta tìm được 6 điểm dao động cùng pha với nhau
→Trên AB có 5 điểm dao động cùng biên độ cùng pha với điểm M cách A một đoạn 1 cm
Với bài toán này, bạn chỉ cần tìm những điểm dao động với biên độ 5mm trên đoạn AB, rồi x2 lên.
A B M d1 d2
Bước sóng: \(\lambda=1,5cm\)
Do biên độ của M là 5mm, nên sóng do A và B truyền đến M vuông pha nhau (\(3^2+4^2=5^2\))
Suy ra: \(d_2-d_1=\left(k+0,5\right)\frac{\lambda}{2}\)
\(-10\le d_2-d_1\le10\Leftrightarrow-10\le\left(k+0,5\right)\frac{\lambda}{2}\le10\Leftrightarrow-10\le\left(k+0,5\right)\frac{1,5}{2}\le10\Leftrightarrow-13,83\le k\le12,83\)
Suy ra: k = -13;-12,....; 11;12
Có 26 điểm thỏa mãn.
Như vậy có 26x2 = 52 điểm dao động với biên độ 5cm trên parabol.
Số điểm cực đại trên đoạn AG là số giá trị k thỏa mãn \(-AG \leq (k+\frac{\triangle \phi}{2\pi})\lambda \leq AG \Rightarrow -\frac{AB}{4}.3=10.875cm \leq (k+0.5)\lambda \leq 10.875\\ \Rightarrow -5.94 \leq k \leq 4.94 \Rightarrow k = -5,-4,\ldots,0,1,\ldots,4\)
có 10 điểm dao động cực đại trên đoạn AG
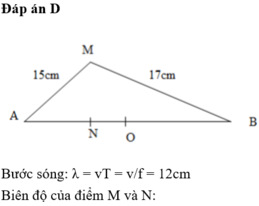
Đáp án D
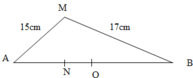
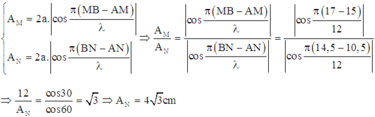
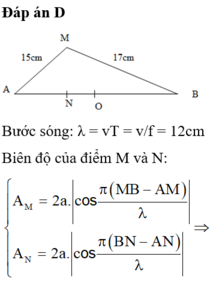
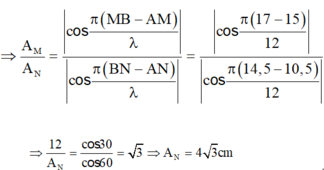
Bước sóng: λ = vT = v/f = 12cm
Biên độ của điểm M và N:
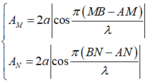
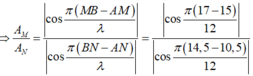
1.
gọi M là vị trí cách S1 là d1 và S2 là d2
 "u_1M=3cos(40\pi.t+\frac{\pi}{6}-\frac{2\pi.d_1}{\lambda})")
 "u_2M=4cos(40\pi.t+2\frac{\pi}{3}-\frac{2\pi.d_2}{\lambda})")
%7D%7B%5Clambda%7D%20+%20%5Cfrac%7B%5Cpi%7D%7B2%7D=(k+1/2)%5Cpi "2\pi.\frac{(d1-d2)}{\lambda} + \frac{\pi}{2}=(k+1/2)\pi")
.
để uM có biên độ là 5 thì u_1M phải vuông pha u_2M ==>
==> d1-d2=k
- Xét 1/2 vòng tròn : -8<=d1-d2<=8 ==> có 17 kể cả 2 điểm trên S1S2
==. 1/2 vòng còn lại có 15 vậy tổng có 32 điểm
2.
6 nút(cả 2 đầu) thì có 5 bó sóng
tính bước sóng:
như vậy điểm M nằm trên bó sóng thứ nhất
trên 1 bó sóng các điểm không phải là bụng hoặc nút thì sẽ có 2 điểm dao động với cùng biên độ đối xứng nhau qua bụng sóng
các điểm trên 1 bó sóng thì dao động cùng pha, 2 bó sóng cạnh nhau thi dao động ngược pha nhau
các bó sóng1,2,3,4,5
vây bó sóng 3, 5 dao động cùng pha với bó sóng 1---> các điểm cần tìm là 1+2+2=5 điểm(diểm 1 là trên bó sóng 1)