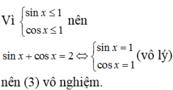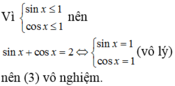K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VD
2
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2020
2.
\(y'=1+\left(m+1\right)cosx\le0;\forall x\in R\)
\(\Leftrightarrow\left(m+1\right)cosx\le-1\) ; \(\forall x\in R\)
- Với \(m=-1\) không thỏa mãn
- Với \(m>-1\Leftrightarrow cosx\le-\frac{1}{m+1}\)
\(\Rightarrow-\frac{1}{m+1}\ge1\Leftrightarrow m+1\le-1\Rightarrow m\le-2\) (ktm)
- Với \(m< -1\Leftrightarrow cosx\ge-\frac{1}{m+1}\Rightarrow-\frac{1}{m+1}\le-1\)
\(\Leftrightarrow m+1\ge1\Rightarrow m\ge0\) (ktm)
Vậy không tồn tại m để hàm đồng biến trên TXĐ
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 8 2020
1.
\(y'=\left(2m+3\right)cosx+2-m\ge0;\forall x\)
\(\Leftrightarrow\left(2m+3\right)cosx\ge m-2\)
- Với \(m=-\frac{3}{2}\) thỏa mãn
- Với \(m>-\frac{3}{2}\Rightarrow cosx\ge\frac{m-2}{2m+3}\)
\(\Rightarrow\frac{m-2}{2m+3}\le\min\limits_Rcosx=-1\) \(\Leftrightarrow3m\le-1\Rightarrow m\le-\frac{1}{3}\Rightarrow-\frac{3}{2}< m\le-\frac{1}{3}\)
- Với \(m< -\frac{3}{2}\Rightarrow cosx\le\frac{m-2}{2m+3}\Rightarrow\frac{m-2}{2m+3}\ge\max\limits_Rcosx=1\)
\(\Leftrightarrow m-2\le2m+3\Rightarrow m\ge-5\)
Kết hợp lai ta được \(-5\le m\le-\frac{1}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 3 2019
Đề thế này hả bạn?
\(A=\int\limits^{\frac{\pi}{2}}_0\frac{\sqrt{sinx}}{\sqrt{sinx}+\sqrt{cosx}}dx\) (1)
Đặt \(\frac{\pi}{2}-x=t\Rightarrow dx=-dt;\left\{{}\begin{matrix}x=0\Rightarrow t=\frac{\pi}{2}\\x=\frac{\pi}{2}\Rightarrow t=0\end{matrix}\right.\)
\(A=\int\limits^0_{\frac{\pi}{2}}\frac{\sqrt{cost}}{\sqrt{cost}+\sqrt{sint}}\left(-dt\right)=\int\limits^{\frac{\pi}{2}}_0\frac{\sqrt{cost}}{\sqrt{sint}+\sqrt{cost}}dt=\int\limits^{\frac{\pi}{2}}_0\frac{\sqrt{cosx}}{\sqrt{sinx}+\sqrt{cosx}}dx\) (2)
Cộng vế với vế của (1) và (2):
\(2A=\int\limits^{\frac{\pi}{2}}_0\frac{\sqrt{sinx}}{\sqrt{sinx}+\sqrt{cosx}}dx+\int\limits^{\frac{\pi}{2}}_0\frac{\sqrt{cosx}}{\sqrt{sinx}+\sqrt{cosx}}dx=\int\limits^{\frac{\pi}{2}}_0\frac{\sqrt{sinx}+\sqrt{cosx}}{\sqrt{sinx}+\sqrt{cosx}}dx=\int\limits^{\frac{\pi}{2}}_0dx=\frac{\pi}{2}\)
\(\Rightarrow A=\frac{\pi}{4}\)
b/ \(B=\int\limits^{\frac{\pi}{2}}_0\frac{\sqrt{cosx}}{\sqrt{cosx}+\sqrt{sinx}}dx\)
Từ (2) ta thấy \(B=A=\frac{\pi}{4}\)
LD
0
12 tháng 1 2017
\(\int\frac{1}{sin^2-4cos^2x}dx=\int\frac{\frac{dx}{cos^2x}}{tan^2x-4}\)
\(=\int\frac{1}{tan^2x-4}d\left(tanx\right)=\int\frac{d\left(tanx\right)}{\left(tanx-2\right)\left(tanx+2\right)}\\ =\frac{1}{4}\int\left(\frac{1}{tanx-2}-\frac{1}{tanx+2}\right)d\left(tanx\right)\\ =\frac{1}{4}\left(ln\left|tanx-2\right|-ln\left|tanx+2\right|\right)+C\\ =\frac{1}{4}ln\left|\frac{tanx-2}{tanx+2}\right|+C\)
HN
1
AH
Akai Haruma
Giáo viên
1 tháng 3 2018
Lời giải:
Ta có:
\(\int ^{\frac{\pi}{2}}_{0}\frac{\sin x}{(\sin x+\cos x)^3}dx=\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{\sin x}{(\sin x+\cos x)^3}dx+\int ^{\frac{\pi}{4}}_{0}\frac{\sin x}{(\sin x+\cos x)^3}dx\)
\(=A+B\)
Xét riêng rẽ:
\(A=\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{\sin^3 x}{(\sin x+\cos x)^3}.\frac{dx}{\sin ^2x}=\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{1}{\left(\frac{\sin x+\cos x}{\sin x}\right)^3}d(-\cot x)\)
\(=\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{1}{(\cot x+1)^3}d(-\cot x)=-\int ^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{d(\cot x+1)}{(\cot x+1)^3}\)
\(=\left.\begin{matrix} \frac{\pi}{2}\\ \frac{\pi}{4}\end{matrix}\right|\frac{1}{2(\cot x+1)^2}=\frac{3}{8}\)
\(B=\int ^{\frac{\pi}{4}}_{0}\frac{\sin x+\cos x-\cos x}{(\sin x+\cos x)^3}dx\)\(=\int ^{\frac{\pi}{4}}_{0}\frac{ 1}{(\sin x+\cos x)^2}dx-\int ^{\frac{\pi}{4}}_{0}\frac{\cos x}{(\sin x+\cos x)^3}dx\)
\(=\int ^{\frac{\pi}{4}}_{0}\frac{1}{\left(\frac{\sin x+\cos x}{\cos x}\right)^2}.\frac{dx}{\cos ^2x}-\int ^{\frac{\pi}{4}}_{0}\frac{1}{\left(\frac{\sin x+\cos x}{\cos^3 x}\right)^3}.\frac{dx}{\cos ^2x}\)
\(=\int ^{\frac{\pi}{4}}_{0}\frac{d(\tan x)}{(\tan x+1)^2}-\int ^{\frac{\pi}{4}}_{0}\frac{d(\tan x)}{(\tan x+1)^3}\)
\(=\int ^{\frac{\pi}{4}}_{0}\frac{d(\tan x+1)}{(\tan x+1)^2}-\int ^{\frac{\pi}{4}}_{0}\frac{d(\tan x+1)}{(\tan x+1)^3}\)
\(=\left.\begin{matrix} \frac{\pi}{4}\\ 0\end{matrix}\right|\frac{-1}{\tan x+1}+\left.\begin{matrix} \frac{\pi}{4}\\ 0\end{matrix}\right|\frac{1}{2(\tan x+1)^2}=\frac{1}{8}\)
Do đó: \(\int ^{\frac{\pi}{2}}_{0}\frac{\sin x}{(\sin x+\cos x)^3}dx=\frac{3}{8}+\frac{1}{8}=\frac{1}{2}\)
Sở dĩ phải chia tích phân thành tổng nhỏ như vậy là do khi ta thực hiện chia sin x xuống dưới mẫu thì hàm số không liên tục trong đoạn \([\frac{\pi}{2}; 0]\)
TC
1
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 2 2020
\(I=\int\frac{dx}{1+cosx}+\int\frac{sinxdx}{1+cosx}=\int\frac{d\left(\frac{x}{2}\right)}{cos^2\frac{x}{2}}-\int\frac{d\left(1+cosx\right)}{1+cosx}\)
\(=tan\frac{x}{2}-ln\left(1+cosx\right)+C\)