Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số lần bắn được 8 là x
Số lần bắn được 6 là y (x,y\(\in\)N* )
Tổng số lần bắn là 100 . Ta có PT
25+42+x+15+y=100
\(\Leftrightarrow\)x+y=18 (1)
Điểm số trung bình là 8,69 nên ta có PT:
\(\dfrac{10.25+9.42+8x+7.15+6y}{100}=8,69\)
\(\Leftrightarrow\)4x+3y=68(2)
Từ (1) , (2) ta có hệ \(\left\{{}\begin{matrix}x+y=18\\4x+3y-68\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=14\\y=4\end{matrix}\right.\)tmđk
Vậy số lần bắn được điểm 8 là 14 lần
Số lần bắn được điểm 6 là 4 lần

+) Thay giá trị của xx vào biểu thức của hàm số y=0,5xy=0,5x, ta được:
f(−2,5)=0,5.(−2,5)=−1,25f(−2,5)=0,5.(−2,5)=−1,25.
f(−2,25)=0,5.(−2,25)=−1,125f(−2,25)=0,5.(−2,25)=−1,125.
f(−1,5)=0,5.(−1,5)=−0,75f(−1,5)=0,5.(−1,5)=−0,75.
f(−1)=0,5.(−1)=−0,5f(−1)=0,5.(−1)=−0,5.
f(0)=0,5.0=0f(0)=0,5.0=0.
f(1)=0,5.1=0,5f(1)=0,5.1=0,5.
f(1,5)=0,5.1,5=0,75f(1,5)=0,5.1,5=0,75.
f(2,2,5)=0,5.2,25=1,125f(2,2,5)=0,5.2,25=1,125.
f(2,5)=0,5.2,5=1,25f(2,5)=0,5.2,5=1,25.
+) Thay giá trị của xx vào biểu thức của hàm số y=0,5x+2y=0,5x+2, ta được:
f(−2,5)=0,5.(−2,5)+2=−1,25+2=0,75f(−2,5)=0,5.(−2,5)+2=−1,25+2=0,75.
f(−2,25)=0,5.(−2,25)+2=−1,125+2=0,875f(−2,25)=0,5.(−2,25)+2=−1,125+2=0,875.
f(−1,5)=0,5.(−1,5)+2=−0,75+2=1,25f(−1,5)=0,5.(−1,5)+2=−0,75+2=1,25.
f(−1)=0,5.(−1)+2=−0,5+2=1,5f(−1)=0,5.(−1)+2=−0,5+2=1,5.
f(0)=0,5.0+2=0+2=2f(0)=0,5.0+2=0+2=2.
f(1)=0,5.1+2=0,5+2=2,5f(1)=0,5.1+2=0,5+2=2,5.
f(1,5)=0,5.1,5+2=0,75+2=2,75f(1,5)=0,5.1,5+2=0,75+2=2,75.
f(2,2,5)=0,5.2,25+2=1,125+2=3,125f(2,2,5)=0,5.2,25+2=1,125+2=3,125.
f(2,5)=0,5.2,5+2=1,25+2=3,25f(2,5)=0,5.2,5+2=1,25+2=3,25.
Vậy ta có bảng sau:
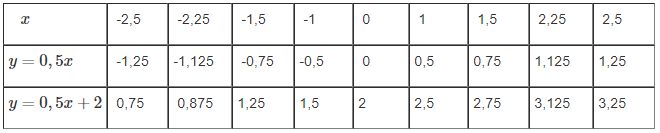
b)
Khi xx lấy cùng một giá trị của xx thì giá trị của hàm số y=0,5x+2y=0,5x+2 lớn hơn giá trị của hàm số y=0,5xy=0,5x là 22 đơn vị.
a)
| x | -2,5 | -2,25 | -1,5 | -1 | 0 | 1 | 1,5 | 2,25 | 2,5 |
| y=0,5x | -1,25 | -1,125 | -0,75 | -0,5 | 0 | 0,5 | 0,75 | 1,125 | 1,25 |
| y=0,5x+2 | 0,75 | 0,875 | 1,25 | 1,5 | 2 | 2,5 | 2,75 | 3,125 | 3,25 |
b) Với các giá trị biến x như nhau thì hàm số y=0,5x+2 luôn lớn hơn hàm số y=0,5x hai đơn vị

a) Ta có y=f(x)=−1/2x+3y=f(x)=−1/2x+3.
Với y=−1/2x+3y=−1/2x+3 thay các giá trị của xx vào biểu thức của yy, ta được:
+) f(−2,5)=−1/2.(−2,5)+3f(−2,5)=−1/2.(−2,5)+3
=(−0,5).(−2,5)+3=(−0,5).(−2,5)+3=1,25+3=4,25=1,25+3=4,25
+) f(−2)=−1/2.(−2)+3f(−2)=−1/2.(−2)+3
=(−0,5).(−2)+3=1+3=4=(−0,5).(−2)+3=1+3=4.
+) f(−1,5)=−1/2.(−1,5)+3f(−1,5)=−1/2.(−1,5)+3
=(−0,5).(−1,5)+3=(−0,5).(−1,5)+3=0,75+3=3,75=0,75+3=3,75.
+) f(−1)=−1/2.(−1)+3f(−1)=−1/2.(−1)+3
=(−0,5).(−1)+3=0,5+3=3,5=(−0,5).(−1)+3=0,5+3=3,5.
+) f(−0,5)=−1/2.(−0,5)+3f(−0,5)=−1/2.(−0,5)+3
=(−0,5).(−0,5)+3=(−0,5).(−0,5)+3=0,25+3=3,25=0,25+3=3,25.
+) f(0)=−1/2.0+3f(0)=−1/2.0+3=(−0,5).0+3=0+3=3=(−0,5).0+3=0+3=3
+) f(0,5)=−1/2.0,5+3f(0,5)=−1/2.0,5+3
=(−0,5).0,5+3=(−0,5).0,5+3=−0,25+3=2,75=−0,25+3=2,75
+) f(1)=−1/2.1+3f(1)=−1/2.1+3
=(−0,5).1+3=−0,5+3=2,5=(−0,5).1+3=−0,5+3=2,5.
+) f(1,5)=−1/2.1,5+3f(1,5)=−1/2.1,5+3
=(−0,5).1,5+3=−0,75+3=(−0,5).1,5+3=−0,75+3=2,25=2,25
+) f(2)=−1/2.2+3f(2)=−1/2.2+3
=(−0,5).2+3=−1+3=2=(−0,5).2+3=−1+3=2.
+) f(2,5)=−1/2.2,5+3f(2,5)=−1/2.2,5+3
=(−0,5).2,5+3=−1,25+3=(−0,5).2,5+3=−1,25+3=1,75=1,75
Ta có bảng sau:

b)
Nhìn vào bảng giá trị của hàm số ở câu a ta thấy khi xx càng tăng thì giá trị của f(x)f(x) càng giảm. Do đó hàm số nghịch biến trên R
a)
| xx | -2,5−2,5 | -2−2 | -1,5−1,5 | -1−1 | -0,5−0,5 | 00 | 0,50,5 | 11 | 1,51,5 | 22 | 2,52,5 |
| y=-\dfrac{1}{2} x+3y=− \(\dfrac{1}{2}\)x+3 |
4,254,25 | 44 | 3,753,75 | 3,53,5 | 3,253,25 | 33 | 2,752,75 | 2,52,5 | 2,252,25 | 22 | 1,751,75 |
b) Khi xx lần lượt nhận các giá trị tăng lên thì giá trị tương ứng của hàm số lại giảm đi. Vậy hàm số đã cho nghịch biến trên \mathbb{R}R.
 Đinh Việt Hoàng
Đinh Việt Hoàng