Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình đa giác TenDaGiac2: DaGiac[B, A, 3] Hình đa giác TenDaGiac3: DaGiac[A, C, 3] Đoạn thẳng c: Đoạn thẳng [A, B] của Hình tam giác TenDaGiac1 Đoạn thẳng a: Đoạn thẳng [B, C] của Hình tam giác TenDaGiac1 Đoạn thẳng b: Đoạn thẳng [C, A] của Hình tam giác TenDaGiac1 Đoạn thẳng f: Đoạn thẳng [B, A] của Hình đa giác TenDaGiac2 Đoạn thẳng g: Đoạn thẳng [A, D] của Hình đa giác TenDaGiac2 Đoạn thẳng h: Đoạn thẳng [D, B] của Hình đa giác TenDaGiac2 Đoạn thẳng i: Đoạn thẳng [A, C] của Hình đa giác TenDaGiac3 Đoạn thẳng j: Đoạn thẳng [C, E] của Hình đa giác TenDaGiac3 Đoạn thẳng k: Đoạn thẳng [E, A] của Hình đa giác TenDaGiac3 Đoạn thẳng n: Đoạn thẳng [E, F] Đoạn thẳng p: Đoạn thẳng [D, F] Đoạn thẳng q: Đoạn thẳng [F, C] Đoạn thẳng r: Đoạn thẳng [F, B] A = (-1.38, 6.9) A = (-1.38, 6.9) A = (-1.38, 6.9) B = (-2.52, 4.02) B = (-2.52, 4.02) B = (-2.52, 4.02) C = (1.98, 4.04) C = (1.98, 4.04) C = (1.98, 4.04) Điểm D: DaGiac[B, A, 3] Điểm D: DaGiac[B, A, 3] Điểm D: DaGiac[B, A, 3] Điểm E: DaGiac[A, C, 3] Điểm E: DaGiac[A, C, 3] Điểm E: DaGiac[A, C, 3] Điểm F: Giao điểm của l, m Điểm F: Giao điểm của l, m Điểm F: Giao điểm của l, m 60 o
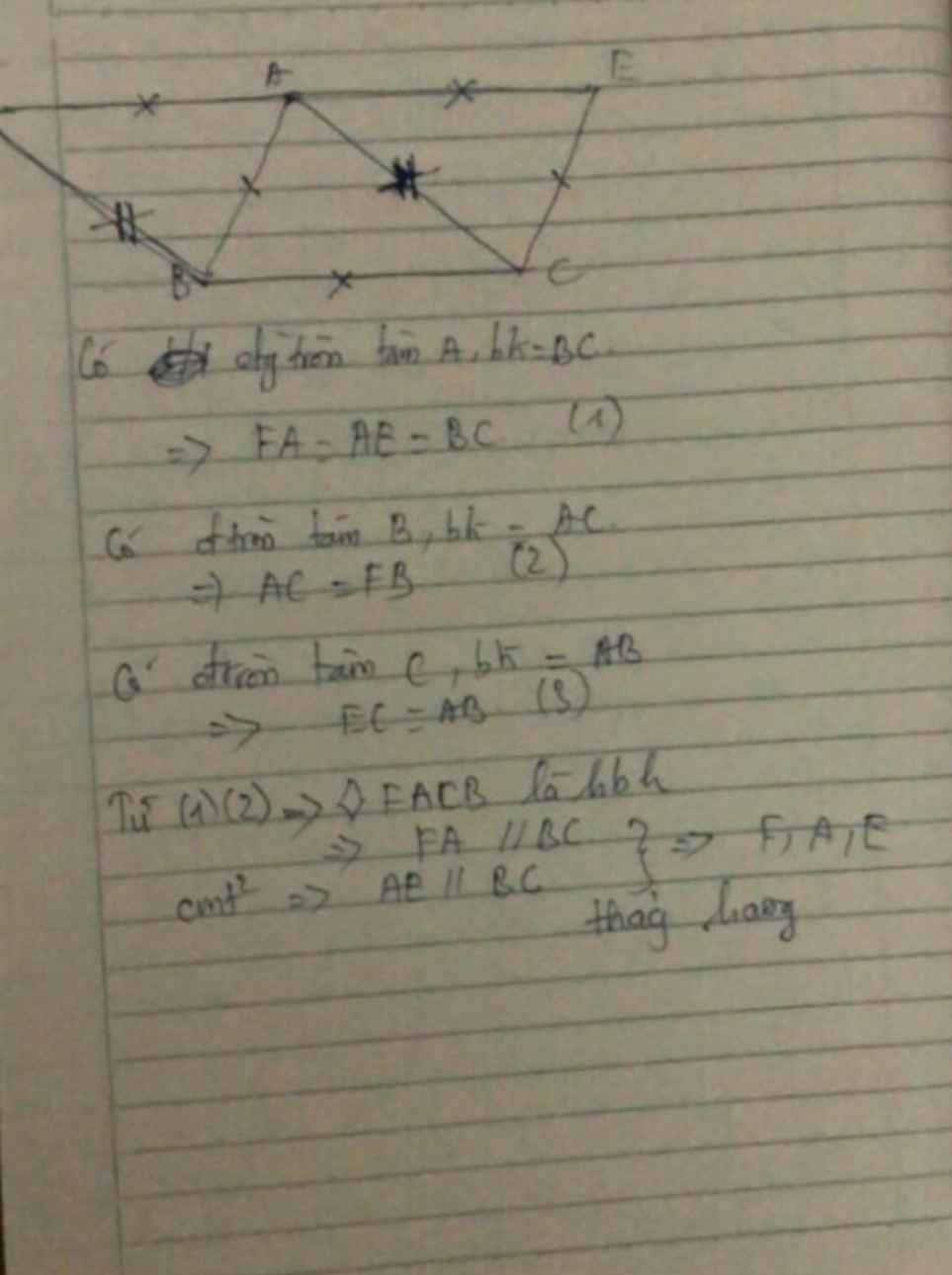
Xét tứ giác ADFE có các cặp cạnh đối bằng nhau nên nó là hình bình hành. Vậy thì \(\widehat{FDA}=\widehat{FEA}\)
Suy ra \(\widehat{BDF}=\widehat{FDA}+60^o=\widehat{FEA}+60^o=\widehat{FEC}\)
Xét tam giác BDF và tam giác FEC có: BD = EF ; DF = EC; \(\widehat{BDF}=\widehat{FEC}\)
\(\Rightarrow\Delta BDF=\Delta FEC\left(c-g-c\right)\Rightarrow BF=CF\) . Vậy FBC là tam giác cân.
Ta thấy theo tính chất hình bình hành: \(\widehat{DFE}=180^o-\widehat{FEA}\) (1)
Lại có : \(\widehat{DFE}=\widehat{DFB}+\widehat{BFC}+\widehat{EFC}=\widehat{BFC}+\left(\widehat{DFB}+\widehat{EFC}\right)\)
\(=\widehat{BFC}+\left(\widehat{ECF}+\widehat{EFC}\right)\)
\(=\widehat{BFC}+\left(180^o-60^o-\widehat{FEA}\right)=\widehat{BFC}+120^o-\widehat{FEA}\) (2)
Từ (1) và (2) suy ra \(\widehat{BFC}=60^o\)
Suy ra FBC là tam giác đều.

a: xét tam giác abc và tam giác abd có
- ab chung
- ac=ad
- cd=bd
suy ra tam gics abc= tam giác abd (c-c-c)
b:xét tam giác acd và tam giác bcd có
-cd chung
- ac=ad
- cb=bd
suy ra tam giác acd= tam giác bcd (c-c-c)