Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mấy bài kia mình giải cho bạn rùi bây giờ mk giải bài 4 nhá
Gọi số nguyên cần tìm là \(a\) theo đề bài ta có :
\(\frac{151-a}{161-a}=\frac{21}{26}\)
\(\Rightarrow\)\(21\left(161-a\right)=26\left(151-a\right)\)
\(\Rightarrow\)\(3381-21a=3926-26a\)
\(\Rightarrow\)\(-21a+26a=3926-3381\)
\(\Rightarrow\)\(5a=545\)
\(\Rightarrow\)\(a=\frac{545}{5}\)
\(\Rightarrow\)\(a=109\)
Vậy số nguyên cần tìm là \(109\)
Chúc bạn học tốt ~

gọi 2 số là a, b.có a/b=3/4; a+60/b=9/10
a/b=3/4 => 3a=4b
a+60/b=9/10 => 10a+600=9b
=>27a=36b
=>40a+2400=36b
=>27a=40a+2400
=>x=....
=>y=...
có thể nó sai
Gọi phân số ban đầu là \(\frac{a}{b}\) theo đề bài ta có :
\(\frac{a}{b}=\frac{3}{4}\)
Đề bài cho : \(\frac{a+60}{b}=\frac{9}{10}\)\(\Rightarrow\)\(\frac{a}{b}+\frac{60}{b}=\frac{9}{10}\)
Thay \(\frac{a}{b}=\frac{3}{4}\) vào \(\frac{a}{b}+\frac{60}{b}=\frac{9}{10}\) ta được : \(\frac{3}{4}+\frac{60}{b}=\frac{9}{10}\)
\(\Leftrightarrow\)\(\frac{60}{b}=\frac{9}{10}-\frac{3}{4}\)
\(\Leftrightarrow\)\(\frac{60}{b}=\frac{3}{20}\)
\(\Leftrightarrow\)\(b=60:\frac{3}{20}\)
\(\Leftrightarrow\)\(b=\frac{60.20}{3}\)
\(\Leftrightarrow\)\(b=400\)
Mà \(\frac{a}{b}=\frac{3}{4}\)\(\Rightarrow\)\(\frac{a}{400}=\frac{3}{4}\)\(\Rightarrow\)\(a=\frac{3}{4}.400=300\)
Vậy phân số ban đầu là \(\frac{300}{400}\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

Nếu:
\(\dfrac{a}{b}< 1\Rightarrow\dfrac{a+m}{b+m}< 1\left(m\in N\right)\)
\(A=\dfrac{2005^{2005}+1}{2005^{2006}+1}< 1\)
\(A< \dfrac{2005^{2005}+1+2004}{2005^{2006}+1+2004}\Rightarrow A< \dfrac{2005^{2005}+2005}{2005^{2006}+2005}\Rightarrow A< \dfrac{2005\left(2005^{2004}+1\right)}{2005\left(2005^{2005}+1\right)}\Rightarrow A< \dfrac{2005^{2004}+1}{2005^{2005}+1}=B\)
\(A< B\)
Ta có : A = \(\dfrac{2005^{2005}+1}{2005^{2006}+1}\)
\(2005\)A = \(\dfrac{\left(2005^{2005}+1\right).2005}{2005^{2006}+1}\)
\(2005\)\(A\)= \(\dfrac{2005^{2006}+2005}{2005^{2006}+1}\)
\(2005\)\(A\)= \(\dfrac{2005^{2006}+1+2004}{2005^{2006}+1}\)
\(2005A=\dfrac{2005^{2006}+1}{2005^{2006}+1}+\dfrac{2004}{2005^{2006}+1}\)
\(2005A=1+\dfrac{2004}{2005^{2006}+1}\)
Tương tự như vậy với \(B\) ta đc
\(2005B=1+\dfrac{2004}{2005^{2005}+1}\)
Vì \(2005^{2006}+1>2005^{2005}+1\)
\(=>\) \(1+\dfrac{2004}{2005^{2006}+1}\)\(< \)\(1+\dfrac{2004}{2005^{2005}+1}\)
\(=>\)\(2005A< 2005B\)
\(=>\)\(A< B\)
Vậy \(A< B\)

\(C=\dfrac{2006\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2007}\right)}{\left(1+\dfrac{2005}{2}\right)+\left(1+\dfrac{2004}{3}\right)+...+\left(1+\dfrac{1}{2006}\right)+1}\)
\(=\dfrac{2006\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2007}\right)}{\dfrac{2007}{2}+\dfrac{2007}{3}+...+\dfrac{2007}{2007}}=\dfrac{2006}{2007}\)
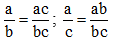


Câu 3:
Gọi phân số cần tìm có dạng là a/b
Vì a/b=3/4 nên a/3=b/4
Đặt a/3=b/4=k
=>a=3k; b=4k
Theo đề, ta có: \(\dfrac{a+60}{b}=\dfrac{9}{10}\)
=>10a+600=9b
=>10a-9b=600
=>30k-36k=600
=>k=-10
=>a/b=-30/-40
Câu 4:
Gọi số cần tìm là x
Theo đề, ta có: \(\dfrac{151-x}{161-x}=\dfrac{21}{26}\)
=>3926-26x=3381-21x
=>-5x=-545
hay x=109