
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{1995.1994-1}{1993.1995+1994}=\dfrac{1995.1994-1}{1993.1995+1994}=\dfrac{1993.1995+1995-1}{1993.1995+1994}=1\)

\(\left(7^{1997}-7^{1995}\right):\left(7.7^{1994}\right)\\ =\left(7^{1997}-7^{1995}\right):\left(7^{1+1994}\right)\\ =\left(7^{1997}-7^{1995}\right):7^{1995}\\ =\left(7^{1997}:7^{1995}\right)-\left(7^{1995}:7^{1995}\right)\\ =\left(7^{1997-1995}\right)-1\\ =7^2-1\\ =48\)

\(\frac{-1997\cdot1996+1}{-1995\cdot-1997+1996}\)=\(\frac{-1996\cdot1997+1}{1995\cdot1997+1997-1}\)=\(\frac{-1996\cdot1997+1}{\left(1995\cdot1997+1997\right)-1}\)=\(\frac{-1996\cdot1997+1}{1996\cdot1997-1}\)

Ta có
\(P=\sqrt{\left(x+1995\right)^2}+\sqrt{\left(x+1996\right)^2}\)
\(\Rightarrow P=\left|x+1995\right|+\left|x+1996\right|\)
\(\Rightarrow P=\left|-x-1995\right|+\left|x+1996\right|\)
Ta có \(\begin{cases}\left|-x-1995\right|\ge-x-1995\\\left|1996+x\right|\ge1996+x\end{cases}\)
\(\Rightarrow\left|-x-1995\right|+\left|x+1996\right|\ge-\left(x+1995\right)+\left(x+1996\right)\)
\(\Leftrightarrow P\ge1\)
Dấu " = " xảy ra khi \(\begin{cases}-\left(x+1995\right)\ge0\\x+1996\ge0\end{cases}\)\(\Leftrightarrow\begin{cases}x\le-1995\\x\ge-1996\end{cases}\)
Vậy MINP=1 khi \(-1996x\le x\le-1995\)
Ta có : \(P=\sqrt{\left(x+1995\right)^2}+\sqrt{\left(x+1996\right)^2}=\left|x+1995\right|+\left|x+1996\right|\)
\(=\left|-x-1995\right|+\left|x+1996\right|\ge\left|-x-1995+x+1996\right|=1\)
Dấu "=" xảy ra \(\Leftrightarrow\begin{cases}-x-1995\ge0\\x+1996\ge0\end{cases}\) \(\Leftrightarrow-1996\le x\le-1995\)
Vậy Min P = 1 <=> \(-1996\le x\le-1995\)

\(A=x^2-y^2-2y-1\)
\(=x^2-\left(y+1\right)^2=\left(x-y-1\right)\left(x+y+1\right)\)
\(=\left(93-6-1\right)\left(93+6+1\right)=86\cdot100=8600\)
B k hiểu đề là j

Công thức tổng quát:n thuộc N
3/((10n+3)(10n+13))
=(3/10)((1/(10n+3))-(1/(10n+13)))
1/13 + 3/(13×23) + 3/(23.33) + ....+3/(1993.2003)
=(3/10)(1/3-1/13+1/13-1/23+...+1/1993-1/2003)
=(3/10)(1/3-1/2003)
=200/2003
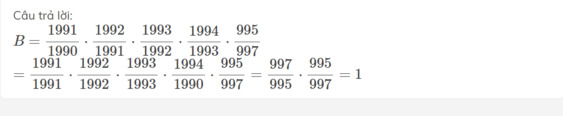
\(=\dfrac{1994\left(1994+1\right)-1}{1994^2-1+1994}=\dfrac{1994^2+1993}{1994^2+1993}=1\)