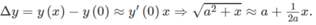K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Tính nhanh ạ
2 tháng 11 2021
Tham khảo: Bài 4.8 trang 211 Sách bài tập Đại số và giải tích 11: Chứng minh rằng với |x| rất bé so với
2 tháng 11 2021
Tham khảo cách giải:
Đặt \(x\left(y\right)=\sqrt{a^2+x}\) ta có:
\(y'\left(x\right)=\dfrac{\left(a^2+x\right)'}{2\sqrt{a^2+x}}=\dfrac{1}{2\sqrt{a^2+x}}\)
Từ đó:
\(\Delta y=y\left(x\right)-y\left(0\right)\approx y'\left(0\right)x\)
\(\Rightarrow\sqrt{a^2+x}-\sqrt{a^2+0}\approx\dfrac{1}{2\sqrt{a^2+0}}x\)
\(\Rightarrow\sqrt{a^2+x}-a\approx\dfrac{x}{2a}\)
\(\Rightarrow\sqrt{a^2+x}\approx a+\dfrac{x}{2a}\)
Áp dụng :
\(\sqrt{146}=\sqrt{12^2+2}\)
\(\approx12+\dfrac{2}{2.12}\approx12,0833\)
JE
2
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 1 2021
\(\left\{{}\begin{matrix}u_1.u_1.q.u_1.q^2=4096\\u_1.\dfrac{q^3-1}{q-1}=56\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(u_1q\right)^3=4096\\u_1\left(q^2+q+1\right)=56\end{matrix}\right.\)
\(\left\{{}\begin{matrix}u_1q=16\\u_1\left(q^2+q+1\right)=56\end{matrix}\right.\)
\(\Rightarrow\dfrac{16}{q}\left(q^2+q+1\right)=56\)
\(\Leftrightarrow16q^2-40q+16=0\Rightarrow\left[{}\begin{matrix}q=1\\q=\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow u_1=8\)
HT
27 tháng 1 2021
\(\left\{{}\begin{matrix}u_1u_1u_1qq^2=4096\\u_1+u_1q+u_1q^2=56\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}u_1^3q^3=4096\\u_1\left(1+q+q^2\right)=56\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}u_1q=16\\u_1\left(1+q+q^2\right)=56\end{matrix}\right.\)
\(\Rightarrow\dfrac{1+q+q^2}{q}=\dfrac{7}{2}\Leftrightarrow2+2q+2q^2=7q\Rightarrow\left[{}\begin{matrix}q=2\\q=\dfrac{1}{2}\left(loai\right)\end{matrix}\right.\)
\(\Rightarrow u_1=\dfrac{16}{2}=8\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
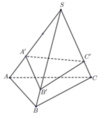
a) • Ta có: M ∈ b và (P) ∩ (Q) = b;
Suy ra M ∈ (P).
Mà M ∈ (M, a)
Do đó M là giao điểm của (P) và (M, a).
Lại có b’ = (P) ∩ (M, a)
Suy ra đường thẳng b’ đi qua M.
Tương tự ta cũng chứng minh được b’’ đi qua điểm M.
• Ta có: a // (P);
a ⊂ (M, a)
(M, a) ∩ (P) = b’
Do đó a // b’.
Tương tự ta cũng có a // b’’.
Do đó b’ // b’’.
Mặt khác: (P) ∩ (Q) = b;
(M, a) ∩ (P) = b’;
(M, a) ∩ (Q) = b’’;
b // b’’.
Do đó b // b’ // b’’.
Mà cả ba đường thẳng cùng đi qua điểm M nên ba đường thẳng này trùng nhau.
b) Vì a // b’ nên a // b (do b ≡ b’).
22 tháng 8 2023
tham khảo
Ta có:\(a//\left(P\right)\)
\(a//\left(Q\right)\)
\(\left(P\right)\cap\left(Q\right)=b\)
Do đó theo hệ quả định lí \(2\) ta có \(a//b\).
9 tháng 1 2023
Gọi ba số hạng liên tiếp lần lượt là a-n;a;a+n
Theo đề, ta có: a-n+a+a+n=27 và (a-n)(a+n)=56
=>a=9 và (9-n)(9+n)=56
=>a=9 và \(n\in\left\{5;-5\right\}\)
3 tháng 2 2022
Bài 3:
Đặt a/5=b/4=k
=>a=5k; b=4k
\(a^2-b^2=1\)
\(\Leftrightarrow9k^2=1\)
\(\Leftrightarrow k^2=\dfrac{1}{9}\)
Trường hợp 1: k=1/3
=>a=5/3; b=4/3
Trường hợp 2: k=-1/3
=>a=-5/3; b=-4/3
