Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chỉ ra điểm C nằm giữa hai điểm A và B. Từ đó tính được BC = 2 cm.
b) Chỉ ra điểm B nằm giữa hai điểm C và D. Từ đó tính được CD = 4 cm.

a)+)Tia BC và BD đối nhau.
\(C\in BC;D\in BD\)
=>Điểm B nằm giữa 2 điểm C và D
\(\Rightarrow BC+BD=CD\)
\(\Rightarrow4+2=CD\)
=>6cm=CD
Vậy CD=6cm
b)+)Điểm M là trung điểm của đoạn thẳng CD
\(\Rightarrow CM=MD=\frac{CD}{2}=\frac{6cm}{2}=3cm\)
\(\Rightarrow CM=MD=3cm\)
+)Trên tia CD ta có:\(DB< DM\)(vì 2cm<3cm)
=>Điểm B nằm giữa 2 điểm M và D
\(\Rightarrow MB+BD=MD\)
\(\Rightarrow MB+2=3\)
\(\Rightarrow MB=3-2=1cm\)
Vậy MB=1cm
c)
d)+)Trên nửa mặt phẳng bờ là đường thẳng AC có chứa điểm D chứa các tia AC;Ax;AB;Ay;AD và n tia chung gốc A phân biệt khác
Do đó số tia là:5+n(tia)
+)Lấy 1 tia hợp với n+4 tia phânchung gốc phân biệt được n+4 góc
+)Có n+5 tia nên có:(n+4).(n+5) góc
+)Nếu tính như trên thì mỗi góc được tính 2 lần.Do đó số góc thực tế là:
\(\frac{\left(n+4\right).\left(n+5\right)}{2}\)góc
Vậy sẽ tạo ra \(\frac{\left(n+4\right).\left(n+5\right)}{2}\)góc gốc Anếu có n+5 tia chung gốc A phân biệt
Phần c bn xem lại nha
Chúc bn học tốt

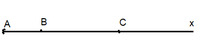
a. ta có :
\(AB+BC=AC\\ hay2+BC=7\\ \Rightarrow BC=7-2=5\left(cm\right)\)
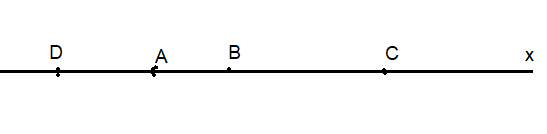
b. ta có :
\(BD-AB=AD\\ hayBD-2=3\\ \Rightarrow BD=3+2=5\left(cm\right)\)
c. ta có :
\(DC-BD=BC\\ hayDC-5=5\\ \Rightarrow DC=5+5=10\left(cm\right)\)
ta thấy \(BD=BC=\dfrac{DC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
nên B là trung điểm DC

A x B C 3 cm 5 cm D
a) Ta có AB < AC nên B nằm giữa hai điểm còn lại.
=> AB + BC = AC
=> 3 cm + BC = 5 cm
=> BC = 5 cm - 3 cm
=> BC = 2 cm
b) Ta có C là trug điểm của BD => BC = CD = 2 cm
=> AD = AB + BC + CD
=> AD = 3 cm + 2 cm + 2 cm
=> AD = 7 cm
2. Tìm các số tự nhiên x sao cho x + 20 là bội của x + 2
x + 20 là bội của x + 2
=> x + 12 + 8 \(⋮\)x + 2
=> 18 \(⋮\)x + 2
=> x + 2 \(\in\) Ư(18) = {1; 2; 3; 6; 9; 18}
x + 2 = 1 => x = -1 (loại)
x + 2 = 2 => x = 0
x + 2 = 3 => x = 1
x + 2 = 6 => x = 4
x + 2 = 9 => x = 7
x + 2 = 18 => x = 16
Vậy x \(\in\) {0; 1; 4; 7; 16}