Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo :
hai vòi nước cùng chảy vào một cái bể không có nước,trong 4h48' sẽ đầy bể.nếu mở vòi thứ nhất trong 3h và vòi thứ hai trong 4h thì được 3/4 bể nước.hỏi mỗi vòi khác chảy thì trong bao lâu mới đầy bể?
Gọi năng suất vòi 1 là x (x>0) (năng suất ở đây hiểu là sau 1 giờ thì vòi 1 chảy được 1 lượng nước nào đó). Gọi năng suất vòi 2 là y (y>0) => năng suất chung cả hai vòi là x+y. Do sau 4,8 giờ (4h48') thì 2 vòi chảy cùng đầy bể nên 1 giờ thì 2 vòi chảy được lượng nước là 1/4,8 bể = 5/24 bể => x+y =5/24 (1). Do mở vòi thứ nhất trong 3h và vòi thứ hai trong 4h thì được 3/4 bể nước nên ta có phương trình 3x+4y=3/4 (bể) (2), từ (1) và (2) => ta có hệ phương trình x+y =5/24 và 3x+4y=3/4. Giải hệ phương trình này ta được x=1/12 và y=1/8. => thời gian chảy đẩy bể của vòi 1 là 1/x = 12h, và tương tự thì vòi 2 là 8h

Gọi thời gian chảy riêng của vòi 1 và vòi 2 lần lượt là a,b
Theo đề, ta có hệ:
1/a+1/b=1/6 và 10/a+4/b=1
=>a=18; b=9

Gọi x (phút), y (phút) lần lượt là thời gian vòi thứ nhất, vòi thứ hai chảy một mình để đầy bể.
(Điều kiện: x, y > 80 )
Trong 1 phút vòi thứ nhất chảy được 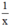 bể; vòi thứ hai chảy được
bể; vòi thứ hai chảy được 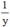 bể.
bể.
Sau 1 giờ 20 phút = 80 phút, cả hai vòi cùng chảy thì đầy bể nên ta có phương trình:
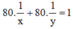
Mở vòi thứ nhất trong 10 phút và vòi thứ 2 trong 12 phút thì chỉ được 2/15 bể nước nên ta có phương trình :
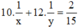
Ta có hệ phương trình:
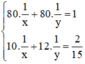
Đặt 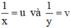 . Khi đó hệ phương trình trở thành :
. Khi đó hệ phương trình trở thành :
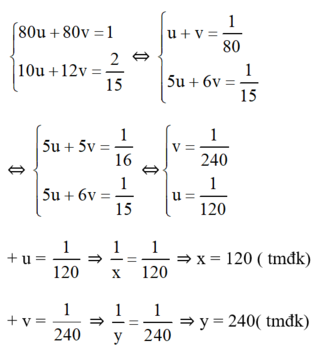
Vậy nếu chảy một mình, để đầy bể vòi thứ nhất chảy trong 120 phút (= 2 giờ) , vòi thứ hai 240 phút (= 4 giờ)

Gọi x (phút), y (phút) lần lượt là thời gian vòi thứ nhất, vòi thứ hai chảy một mình để đầy bể.
(Điều kiện: x, y > 80 )
Trong 1 phút vòi thứ nhất chảy được 1/x bể; vòi thứ hai chảy được 1/y bể.
Sau 1 giờ 20 phút = 80 phút, cả hai vòi cùng chảy thì đầy bể nên ta có phương trình:
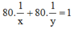
Mở vòi thứ nhất trong 10 phút và vòi thứ 2 trong 12 phút thì chỉ được 2/15 bể nước nên ta có phương trình :
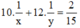
Ta có hệ phương trình:
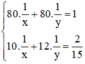
Đặt 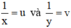 . Khi đó hệ phương trình trở thành :
. Khi đó hệ phương trình trở thành :
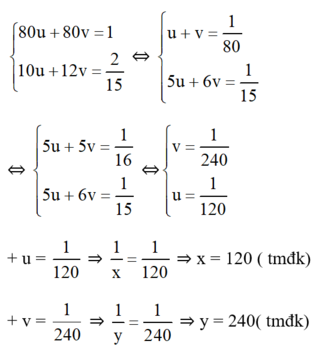
Vậy nếu chảy một mình, để đầy bể vòi thứ nhất chảy trong 120 phút (= 2 giờ) , vòi thứ hai 240 phút (= 4 giờ)
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.

Gọi thời gian vòi thứ nhất chảy riêng đầy bể là x (giờ) (x>6)
thời gian vòi thứ hai chảy riêng đầy bể là y (giờ) (y>6)
Hai vòi nước cùng chảy vào một cái bể không có nước trong 6 giờ thì đầy bể
⇒ 1 x + 1 y = 1 6 (1)
vòi thứ nhất chảy trong 2 giờ, sau đó đóng lại và mở vòi thứ hai chảy tiếp trong 3 giờ nữa thì được 2/5 bể ⇒ 2. 1 x + 3. 1 y = 2 5 (2)
Từ (1) và (2) ta có hệ phương trình 1 x + 1 y = 1 6 2. 1 x + 3. 1 y = 2 5 ⇔ x = 10 y = 15
Đối chiếu với điều kiện, giá trị x=10; y=15 thỏa mãn.
Vậy thời gian vòi thứ nhất chảy riêng đầy bể là 10 giờ, thời gian vòi thứ hai chảy riêng đầy bể là 15 giờ.

Đổi 2 giờ 55 phút = ![]() giờ
giờ
Gọi x (giờ) là thời gian chảy riêng đầy bể của vòi thứ nhất.
Điều kiện: x > 35/12
Khi đó thời gian chảy riêng đầy bể của vòi thứ hai là x + 2 (giờ)
trong 1 giờ, vòi thứ nhất chảy được 1/x (bể)
trong 1 giờ, vòi thứ hai chảy được 1/(x + 2 ) (bể)

Giá trị x = - 7/6 không thỏa mãn điều kiện bài toán.
Vậy vòi thứ nhất chảy riêng đầy bể trong 5 giờ
vòi thứ hai chảy riêng đầy bể trong 5 + 2 = 7 giờ

Để tìm ra thời gian mỗi vòi chảy một mình thì đầy bể, ta có thể sử dụng phương pháp sau:
Tìm ra thời gian hai vòi chảy chung là bao lâu: 4 giờ 48 phút (thời gian hai vòi chảy chung để đầy bể).
Tìm ra thời gian hai vòi chảy riêng là bao lâu: 9 giờ + 5 giờ 12 phút = 14 giờ 12 phút (thời gian hai vòi chảy riêng để đầy bể)
Tìm ra thời gian mỗi vòi chảy một mình: 14 giờ 12 phút / 2 = 7 giờ 6 phút (thời gian mỗi vòi chảy một mình để đầy bể)
Vậy, mỗi vòi chảy một mình trong 7 giờ 6 phút thì đầy bể.

Đổi 6h40p=20/3h ; 4h24p=22/5h
Mỗi giờ vòi I, II chảy được lần lượt x,y lượng nước tỉ lệ so với bể (x,y>0)
Ta có: 20/3 x + 20/3 y = 1 (a)
Bên cạnh đó, vòi I chảy 4h24p và vòi II chảy 2h được 2/3 bể:
=> 22/5 x + 2y = 2/3 (b)
Từ (a), (b) lập hpt:
\(\left\{{}\begin{matrix}\dfrac{20}{3}x+\dfrac{20}{3}y=1\\\dfrac{22}{5}x+2y=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{72}\left(TM\right)\\y=-\dfrac{1}{360}\left(loại\right)\end{matrix}\right.\)
Xem lại đề em ơi

- Gọi phần bể vòi thứ nhất, thứ hai chảy được trong 1 phút lần lượt là \(x,y\left(0< x,y< 1\right)\)
Đổi 1h30p=90p
- Hai vòi nước cùng chảy vào 1 bể cạn thì sau 1h30p đầy bể nên:
\(90\left(x+y\right)=1\Rightarrow x+y=\dfrac{1}{90}\left(1\right)\)
- Vòi 1 chảy trong 15p rồi đến vòi 2 chảy tiếp trong 20p được 1/5 bể nên:
\(15x+20y=\dfrac{1}{5}\left(2\right)\)
(1), (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=\dfrac{1}{90}\\15x+20y=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}15x+15y=\dfrac{1}{6}\\15x+20y=\dfrac{1}{5}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y=\dfrac{1}{90}\\5y=\dfrac{1}{30}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{225}\\y=\dfrac{1}{150}\end{matrix}\right.\)
Thời gian vòi 1 chảy để đầy bể: \(1:\dfrac{1}{225}=225\) phút = 3,75h.
Thời gian vòi 2 chảy để đầy bể: \(1:\dfrac{1}{150}=150\) phút=2,5h.
Để giải quyết bài toán này, chúng ta cần xác định lượng nước mà mỗi vòi chảy vào bể trong một giờ.
Gọi x là lượng nước mà mỗi vòi chảy vào bể trong một giờ. Theo giả thiết, khi mở cả hai vòi trong một giờ, bể sẽ được 1/3 đầy. Vì vậy, lượng nước mà mỗi vòi chảy vào bể trong một giờ là 2x (do có hai vòi).
Theo giả thiết ban đầu, nếu hai vòi cùng chảy vào bể trong 6 giờ, bể sẽ đầy. Với lượng nước mà mỗi vòi chảy vào bể trong một giờ là 2x, ta có:
6 * 2x = 1 (bể đầy)
Từ đó, ta có:
12x = 1
x = 1/12
Vậy, mỗi vòi chảy riêng thì để bể đầy, mỗi vòi sẽ mất 1/12 giờ, hay khoảng 5 phút.
Lưu ý rằng đây là một bài toán giả định, và kết quả phụ thuộc vào giả thiết ban đầu.

gọi tuổi con hiện nay là x thì tuổi mẹ hiện nay là x x 8 , ta có : con / mẹ =x + 10 / x x 8 + 10 / = 1 / 3
= > ( x x 8 + 10 ) x 1 = ( x + 10 ) x 3
x x 8 + 10 = x x 3 + 30 ( 30 = 10 x 3 )
x x 8 - x x 3 = 30 - 10
x x 5 = 20
x = 20 : 5
x = 4 = > tuổi con hiện nay là : 4 tuổi
tuổi mẹ hiện nay là : 4 x 8 = 32 ( tuổi )