Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi số chiếc nón lá mỗi ngày cơ sở đó làm được là x (chiếc)
Số ngày cơ sở đó dự kiến làm hết 300 chiếc nón lá là: 300/x (ngày)
Sau khi làm tăng thêm 5 chiếc nón lá một ngày thì thời gian cơ sở đó làm hết 300 chiếc nón lá là: 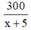 (ngày).
(ngày).
Theo đề bài ta có phương trình:
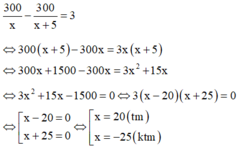
Vậy theo dự kiến, mỗi ngày cơ sở đó làm được 20 chiếc nón lá.

Gọi số mặt nạ mà đội làm dự kiến trong 1 ngày là x(chiếc, x∈N*)
Thời gian hoàn thành công việc nếu đội tăng năng suất lên 10 chiếc mỗi ngày là : \(\dfrac{720}{x+10}\) (ngày)
Thời gian hoàn thành công việc nếu đội giảm năng suất xuống 20 chiếc mỗi ngày là: \(\dfrac{720}{x-20}\) (ngày)
Theo đề bài ra ta có:
\(\dfrac{720}{x-20}-\dfrac{720}{x+10}=4\)
Giải PT trên ta được x=80
Vậy mỗi ngày đội dự định làm 80 chiếc mặt nạ

Lời giải:
Giả sử theo kế hoạch mỗi ngày người đó dự định may $a$ khẩu trang.
ĐK: $a\in\mathbb{N}^*$
Thời gian dự định: $\frac{1000}{a}$ (ngày)
Thực tế:
Mỗi ngày người đó may: $a+30$ (khẩu trang)
Số ngày may: $\frac{1000}{a}-1$ (ngày)
Số khẩu trang thực tế:
$(a+30)(\frac{1000}{a}-1)=1000+170$
$\Leftrightarrow a^2+200a-30000=0$
$\Rightarrow a=100$
Vậy mỗi ngày người đó dự định may 100 khẩu trang.

Gọi số sản phẩm đội dự định làm mỗi ngày là x (x ∈ ℕ * , x < 84) (sản phẩm)
*) Theo kế hoạch, thời gian hoàn thành là 1000/x (ngày)
*) Thực tế, mỗi ngày làm được x + 10 (sản phẩm)
Thời gian hoàn thành 1000/(x+10) (ngày)
Vì thời gian thực tế ít hơn thời gian dự định là 2 ngày nên ta có phương trình:
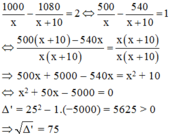
Phương trình có hai nghiệm phân biệt: x 1 = − 25 – 75 = −100 (loại)
và x 2 = −25 + 75 = 50 (tmđk)
Vậy theo kế hoạch, mỗi ngày tổ dự định làm 50 sản phẩm
Đáp án: C

Đổi 30 phút =1/2 h
Gọi năng suất người công nhân theo kế hoạch là x(sản phâm/h) ĐK: \(x>0,x\in N\)
Theo kế hoạch thì thời gian mà người đó hoàn thành 60sp là \(\frac{60}{x}\left(h\right)\)
Nhưng trên thực tế người công nhân đó mỗi giờ làm thêm 2 sản phẩm vậy năng suất thự tế là \(x+2\)(sp/h)
Số sản phẩm mà người đó làm được trên thực tế là \(60+3=63\left(sp\right)\)
Do đó thời gian thực tế mà người đó hoàn thành công việc là \(\frac{63}{x+2}\left(h\right)\)
Vì kế hoạch được hoàn thành sớm hơn dự định 1/2 h nên ta có pt sau:
\(\frac{60}{x}-\frac{63}{x+2}=\frac{1}{2}\)
\(\Leftrightarrow\frac{60x+120}{x\left(x+2\right)}-\frac{63x}{x\left(x+2\right)}=\frac{1}{2}\)
\(\Leftrightarrow\frac{-3x+120}{x^2+2x}=\frac{1}{2}\)
\(\Leftrightarrow x^2+2x=-6x+240\)
\(\Leftrightarrow x^2+8x-240=0\)
\(\Leftrightarrow x^2-12x+20x-240=0\)
\(\Leftrightarrow x\left(x-12\right)+20\left(x-12\right)=0\)
\(\Leftrightarrow\left(x-12\right)\left(x+20\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=12\left(tm\right)\\x=-20\left(loai\right)\end{cases}}\)
Vậy theo kế hoạch mỗi giờ người đó làm được 12 sản phẩm
Gọi số sản phẩm người đó phải hoàn thành theo kế hoạch trong mỗi giờ là a (sản phẩm) (a>0)
Nên số giờ người đó dự định hoàn thành 60 sản phẩm là \(\frac{60}{a}\) (giờ)
Do cải tiến kĩ thuật nên mỗi giờ người đó làm được a+2 (sản phẩm), và còn vượt mức 3 sản phẩm nên thời gian hoàn thành công việc thực tế là \(\frac{60+3}{a+2}\left(giờ\right)\)
Sớm hơn dự định 30 phút = \(\frac{1}{2}\) giờ, nên ta có:
\(\frac{60}{a}-\frac{60+3}{a+2}=\frac{1}{2}\)
\(\Rightarrow\left[60\left(a+2\right)-63a\right]2=a^2+2a\)
\(\Rightarrow a^2+8a-240=0\)
\(\Delta'=4^2+240=256>0\)
\(\Rightarrow a=-4-\sqrt{256}=-20< 0\left(l\right)\)
Hoặc \(a=-4+\sqrt{256}=12\) ( nhận )
Vậy theo kế hoạch mỗi giờ người đó làm 12 sản phẩm.

Lời giải:
Gọi thời gian dự kiến là $a$ ngày thì năng suất dự kiến là $\frac{130}{a}$ sản phẩm / ngày.
Theo bài ra ta có:
Năng suất thực tế: $\frac{130}{a}+2$
Thời gian thực tế: $a-2$
Sản lượng thực tế: $(\frac{130}{a}+2)(a-2)=130+2$
$\Leftrightarrow a-\frac{130}{a}=3$
$\Leftrightarrow a^2-3a-130=0$
$\Rightarrow a=13$ (chọn) hoặc $a=-10$ (loại)
Vậy thời gian dự kiến là $13$ ngày.

Bài 21:
Gọi x (sản phẩm/giờ) là năng suất dự kiến ban đầu của người đó \(\left(x\inℕ^∗\right)\)
=> x + 2 (sản phẩm/giờ) là năng suất lúc sau của người đó
Theo bài ta có phương trình sau:
\(\frac{150}{x}-\frac{1}{2}-2=\frac{150-2x}{x+2}\)
\(\Leftrightarrow300\left(x+2\right)-x\left(x+2\right)-4x\left(x+2\right)=2\left(150-2x\right)x\)
\(\Leftrightarrow300x+600-x^2-2x-4x^2-8x=300x-4x^2\)
\(\Leftrightarrow x^2+10x-600=0\)
\(\Leftrightarrow\left(x-20\right)\left(x+30\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-20=0\\x+30=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=20\left(tm\right)\\x=-30\left(ktm\right)\end{cases}}\)
Vậy ban đầu năng suất người đó là 20 (sản phẩm/giờ)
Bài 22:
Gọi x (sản phẩm/giờ) là năng suất dự kiến của người đó \(\left(x\inℕ^∗;x< 20\right)\)
=> x + 1 (sản phẩm/giờ) là năng suất lúc sau của người đó
Theo bài ra ta có phương trình:
\(\frac{80}{x+1}-\frac{1}{5}=\frac{72}{x}\)
\(\Leftrightarrow400x-x\left(x+1\right)=360\left(x+1\right)\)
\(\Leftrightarrow400x-x^2-x=360x+360\)
\(\Leftrightarrow x^2-39x+360=0\)
\(\Leftrightarrow\left(x-15\right)\left(x-24\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-15=0\\x-24=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=15\left(tm\right)\\x=24\left(ktm\right)\end{cases}}\)
Vậy năng suất ban đầu là 15 sp/giờ

Gọi số sản phẩm người đó mỗi giờ phải làm theo kế hoạch là \(x\)(sản phẩm), \(x>0\).
Theo kế hoạch người đó hoàn thành công việc sau số giờ là: \(\frac{60}{x}\)(giờ)
Đổi: \(30\)phút \(=\)\(0,5\)giờ.
Thực tế mỗi giờ người đó sản xuất được: \(x+2\)(sản phẩm)
Người đó hoàn thành công việc sau: \(\frac{60}{x}-0,5\)(giờ).
Ta có phương trình:
\(\left(x+2\right)\left(\frac{60}{x}-0,5\right)=63\)
\(\Rightarrow-0,5x^2+59x+120=63x\)
\(\Leftrightarrow x^2+8x-240=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=12\left(tm\right)\\x=-20\left(l\right)\end{cases}}\)
mn ơi giúp mình với ạ!!!
2] cao của hình trụ là h (cm)
Đk: h > p
Ta có: Sxq = 2πRh
Stp = 2πRh + 2πR^2
Theo bài ra ta có: Stp = 2Sxq
=> 2πRh + 2πR^2 = 2.2πRh
⇔ 2πR^2 = 2πRh
⇒ h = R = 6 cm
Thể tích V = πR^2.h = π.6^2.6 = 216π (cm3)
Vậy . . .