K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
D
1

NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2022
Lấy \(O\left(0;0\right)\) là 1 điểm thuộc \(d_2\)
\(\Rightarrow d\left(d_1;d_2\right)=d\left(O;d_1\right)=\dfrac{\left|6.0-8.0-101\right|}{\sqrt{6^2+\left(-8\right)^2}}=\dfrac{101}{10}\)

25 tháng 1 2024
a: A(1;2); B(2;1)
=>\(\overrightarrow{AB}=\left(1;-1\right)\)
=>VTPT là (1;1)
Phương trình đường thẳng AB là:
1(x-1)+2(y-1)=0
=>x-1+2y-2=0
=>x+2y-3=0
b:
M(1;3); Δ: 3x+4y+10=0
Khoảng cách từ M đến Δ là:
\(d\left(M;\text{Δ}\right)=\dfrac{\left|1\cdot3+3\cdot4+10\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|3+12+10\right|}{5}=5\)
DN
1


CM
21 tháng 5 2019
Lấy điểm M( x0; 1-2x0) nằm trên d.
Từ giả thiết ta có:
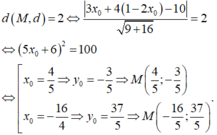
Chọn C.
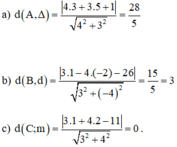
Bài 2:
\(d_M=\dfrac{\left|7\cdot1+10\cdot3-15\right|}{\sqrt{7^2+10^2}}=\dfrac{22}{\sqrt{149}}\)
\(d_N=\dfrac{\left|7\cdot0+10\cdot4-15\right|}{\sqrt{7^2+10^2}}=\dfrac{25}{\sqrt{149}}\)
\(d_P=\dfrac{\left|8\cdot7+0\cdot10-15\right|}{\sqrt{7^2+10^2}}=\dfrac{41}{\sqrt{149}}\)
\(d_Q=\dfrac{\left|7\cdot1+10\cdot5-15\right|}{\sqrt{7^2+10^2}}=\dfrac{42}{\sqrt{149}}\)
Vì 22<25<41<42
nên \(d_M< d_N< d_P< d_Q\)
Do đó: Q cách xa d nhất