Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(\left(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\right)=\left(x,y,z\right)\) với x, y, z > 0 thì ta có \(x+y+z=1\).
Đặt biểu thức ở VT là A. Ta có:
\(A=\sqrt{\dfrac{b^2+2a^2}{a^2b^2}}+\sqrt{\dfrac{c^2+2b^2}{b^2c^2}}+\sqrt{\dfrac{a^2+2c^2}{c^2a^2}}=\sqrt{x^2+2y^2}+\sqrt{y^2+2z^2}+\sqrt{z^2+2x^2}\).
Ta có bất đẳng thức \(\sqrt{a_1^2+a_2^2}+\sqrt{a_3^2+a_4^2}\ge\sqrt{\left(a_1+a_3\right)^2+\left(a_2+a_4\right)^2}\).
Đây là bđt Mincopxki cho hai bộ số thực và dễ dàng cm bằng biến đổi tương đương.
Do đó \(A\ge\sqrt{\left(x+y\right)^2+\left(\sqrt{2}y+\sqrt{2}z\right)^2}+\sqrt{z^2+2x^2}\ge\sqrt{\left(x+y+z\right)^2+\left(\sqrt{2}y+\sqrt{2}z+\sqrt{2}x\right)^2}=\sqrt{1+2}=\sqrt{3}=VP\).
Đẳng thức xảy ra khi a = b = c = 3.
Vậy...
Tương tự: \(GT\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=1\)
\(VT=\dfrac{\sqrt{a^2+a^2+b^2}}{ab}+\dfrac{\sqrt{b^2+b^2+c^2}}{bc}+\dfrac{\sqrt{c^2+a^2+a^2}}{ca}\)
\(VT\ge\dfrac{\sqrt{\dfrac{1}{3}\left(a+a+b\right)^2}}{ab}+\dfrac{\sqrt{\dfrac{1}{3}\left(b+b+c\right)^2}}{bc}+\dfrac{\sqrt{\dfrac{1}{3}\left(c+c+a\right)^2}}{ca}\)
\(VT\ge\sqrt{3}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=\sqrt{3}\)
Dấu "=" xảy ra khi \(a=b=c=3\)

\(\sqrt{\dfrac{ab+2c^2}{1+ab-c^2}}=\sqrt{\dfrac{ab+2c^2}{a^2+b^2+ab}}\)\(=\dfrac{ab+2c^2}{\sqrt{\left(a^2+b^2+ab\right)\left(ab+c^2+c^2\right)}}\)\(\ge\dfrac{2\left(ab+2c^2\right)}{a^2+b^2+2ab+2c^2}\)\(\ge\dfrac{2\left(ab+2c^2\right)}{2\left(a^2+b^2\right)+2c^2}\)\(=\dfrac{ab+2c^2}{a^2+b^2+c^2}\)
\(\Rightarrow\sqrt{\dfrac{ab+2c^2}{1+ab-c^2}}\ge ab+2c^2\)
Tương tự: \(\sqrt{\dfrac{bc+2a^2}{1+bc-a^2}}\ge bc+2a^2\); \(\sqrt{\dfrac{ac+2b^2}{1+ac-b^2}}\ge ac+2b^2\)
Cộng vế với vế \(\Rightarrow VT\ge2a^2+2b^2+2c^2+ab+bc+ac=2+ab+bc+ac\)
Dấu = xảy ra khi \(a=b=c=\dfrac{1}{\sqrt{3}}\)

\(\dfrac{\sqrt{b^2+a^2+a^2}}{ab}\ge\dfrac{\sqrt{\dfrac{1}{3}\left(b+a+a\right)^2}}{ab}=\dfrac{1}{\sqrt{3}}\left(\dfrac{1}{a}+\dfrac{2}{b}\right)\)
Tương tự: \(\dfrac{\sqrt{c^2+2b^2}}{bc}\ge\dfrac{1}{\sqrt{3}}\left(\dfrac{1}{b}+\dfrac{2}{c}\right)\) ; \(\dfrac{\sqrt{a^2+2c^2}}{ac}\ge\dfrac{1}{\sqrt{3}}\left(\dfrac{1}{c}+\dfrac{2}{a}\right)\)
Cộng vế với vế:
\(VT\ge\dfrac{1}{\sqrt{3}}\left(\dfrac{3}{a}+\dfrac{3}{b}+\dfrac{3}{c}\right)=\sqrt{3}\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)=1980\sqrt{3}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{3}{1980}\)

Bài 1:
Áp dụng BĐT AM-GM ta có:
\(a-\dfrac{a^2}{a+b^2}=\dfrac{ab^2}{a+b^2}\le\dfrac{ab^2}{2b\sqrt{a}}=\dfrac{b\sqrt{a}}{2}\)
Tương tự cho các BĐT còn lại cũng có:
\(b-\dfrac{b^2}{b+c^2}\le\dfrac{c\sqrt{b}}{2};c-\dfrac{c^2}{c+a^2}\le\dfrac{a\sqrt{c}}{2}\)
Sau đó cộng theo vế các BĐT trên
\(\dfrac{a^2}{a+b^2}+\dfrac{b^2}{b+c^2}+\dfrac{c^2}{c+a^2}\ge3-\dfrac{1}{2}\left(b\sqrt{a}+c\sqrt{b}+a\sqrt{c}\right)\)
\(\ge3-\dfrac{1}{2}\sqrt{\left(a+b+c\right)\left(ab+bc+ca\right)}\)
\(\ge3-\dfrac{1}{2}\sqrt{\left(a+b+c\right)\cdot\dfrac{\left(a+b+c\right)^2}{3}}=3-\dfrac{3}{2}=\dfrac{3}{2}\)
Đẳng thức xảy ra khi \(a=b=c=1\)
Bài 2:
Áp dụng BĐT AM-GM ta có:
\(\dfrac{a}{\sqrt{2b^2+2c^2-a^2}}=\dfrac{\sqrt{3}a^2}{\sqrt{3a^2\left(2b^2+2c^2-a^2\right)}}\)
\(\ge\dfrac{\sqrt{3}a^2}{\dfrac{3a^2+2b^2+2c^2-a^2}{2}}=\dfrac{\sqrt{3}a^2}{a^2+b^2+c^2}\)
Tương tự cho các BĐT còn lại ta có:
\(\dfrac{b}{\sqrt{2a^2+2c^2-b^2}}\ge\dfrac{\sqrt{3}b^2}{a^2+b^2+c^2};\dfrac{c}{\sqrt{2a^2+2b^2-c^2}}\ge\dfrac{\sqrt{3}c^2}{a^2+b^2+c^2}\)
Cộng theo vế 3 BĐT trên ta có:
\(VT\ge\dfrac{\sqrt{3}\left(a^2+b^2+c^2\right)}{a^2+b^2+c^2}=\sqrt{3}=VP\)
Đẳng thức xảy ra khi \(a=b=c\)

TK: Cho các số thực dương a, b, c thỏa mãn a + b+ c = 3. Chứng minh rằng: \(\sqrt{2a^2+\frac{7}{b^2}}+\sqrt{2b^2+\frac{7}{... - Hoc24

Đề bài sai
Đề đúng: \(\dfrac{1}{\sqrt{a}+2\sqrt{b}+3}+\dfrac{1}{\sqrt{b}+2\sqrt{c}+3}+\dfrac{1}{\sqrt{c}+2\sqrt{a}+3}\le\dfrac{1}{2}\)

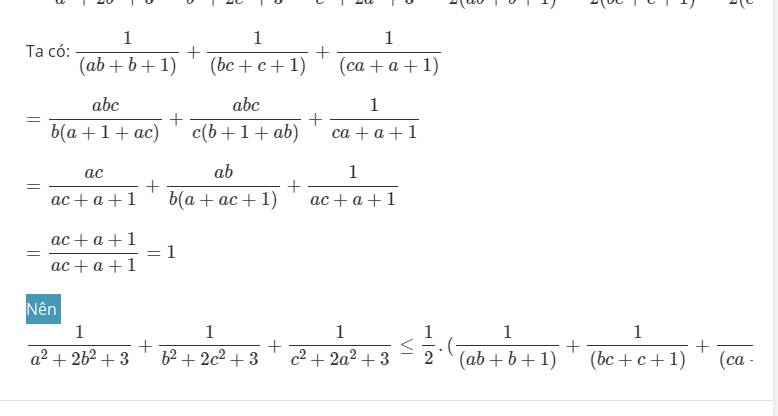

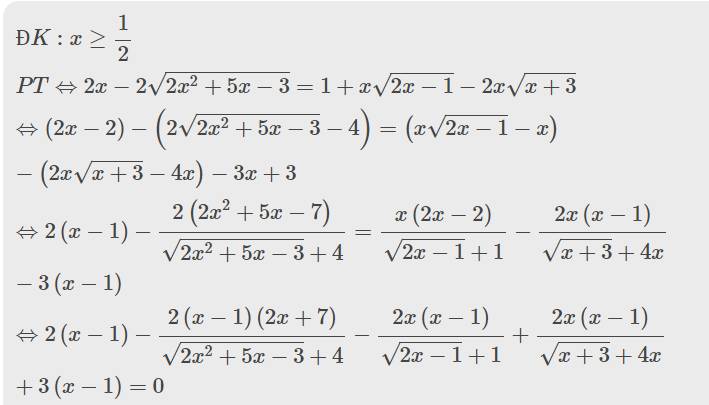


b, \(\frac{a^3}{b+2c}+\frac{b^3}{c+2a}+\frac{c^3}{a+2b}\ge1\)
\(\frac{a^4}{ab+2ac}+\frac{b^4}{bc+2ab}+\frac{c^4}{ac+2bc}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac+2ac+2ab+2bc}\)( Bunhia dạng phân thức )
mà \(a^2+b^2+c^2\ge ab+bc+ac\)
\(=\frac{\left(ab+bc+ac\right)^2}{3+2\left(ab+ac+bc\right)}=\frac{9}{3+6}=1\)( đpcm )
1.
Điều kiện x \ge \dfrac14x≥41.
Phương trình tương đương với \left(\sqrt2.\sqrt{2x^2+x+1}-2\right)-\left(\sqrt{4x-1}-1\right)+2x^2+3x-2 = 0(2.2x2+x+1−2)−(4x−1−1)+2x2+3x−2=0 \Leftrightarrow \dfrac{4x^2+2x-2}{\sqrt2.\sqrt{2x^2+x+1}+2} - \dfrac{4x-2}{\sqrt{4x-1}+1} + (x+2)(2x-1) = 0⇔2.2x2+x+1+24x2+2x−2−4x−1+14x−2+(x+2)(2x−1)=0\\ \Leftrightarrow (2x-1)\left(\dfrac{2(x+1)}{\sqrt2 \sqrt{2x^2+x+1}+2} - \dfrac2{\sqrt{4x-1}+1} + x + 2\right) = 0⇔(2x−1)(22x2+x+1+22(x+1)−4x−1+12+x+2)=0
\Leftrightarrow \left[\begin{aligned} & x =\dfrac12\\ & \dfrac{2(x+1)}{\sqrt2 \sqrt{2x^2+x+1}+2} - \dfrac2{\sqrt{4x-1}+1} + x + 2 = 0\\ \end{aligned}\right.⇔⎣⎢⎢⎢⎡x=2122x2+x+1+22(x+1)−4x−1+12+x+2=0
Với x \ge \dfrac14x≥41 ta có:
\dfrac{2(x+1)}{\sqrt2 \sqrt{2x^2+x+1}+2} > 022x2+x+1+22(x+1)>0
- \dfrac2{\sqrt{4x-1}+1} \ge -2−4x−1+12≥−2
x + 2 > 2x+2>2.
Suy ra \dfrac{2(x+1)}{\sqrt2 \sqrt{2x^2+x+1}+2} - \dfrac2{\sqrt{4x-1}+1} + x + 2 > 022x2+x+1+22(x+1)−4x−1+12+x+2>0.
Vậy phương trình có nghiệm duy nhất x = \dfrac12.x=21.
2.
Đặt P = \dfrac{a^3}{b+2c} + \dfrac{b^3}{c+2a} + \dfrac{c^3}{a+2b}P=b+2ca3+c+2ab3+a+2bc3
Áp dụng bất đẳng thức Cauchy cho hai số dương \dfrac{9a^3}{b + 2c}b+2c9a3 và (b+2c)a(b+2c)a ta có
\dfrac{9a^3}{b+2c} + (b+2c)a \ge 6a^2b+2c9a3+(b+2c)a≥6a2.
Tương tự \dfrac{9b^3}{c+2a} + (c+2a)b \ge 6b^2c+2a9b3+(c+2a)b≥6b2, \dfrac{9c^3}{a+2b} + (a+2b)c \ge 6c^2a+2b9c3+(a+2b)c≥6c2.
Cộng các vế ta có 9P + 3(ab+bc+ca) \ge 6(a^2+b^2+c^2)9P+3(ab+bc+ca)≥6(a2+b2+c2).
Mà a^2+b^2+c^2 \ge ab+bc+ca = 4a2+b2+c2≥ab+bc+ca=4 nên P \ge 1P≥1 (ta có đpcm).