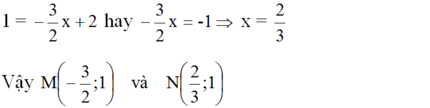Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có $|x_M|=6\Rightarrow x_M=\pm 6
$\Rightarrow y_M=ax_M+b=\pm 6a+b$
Vậy $M(6,6a+b)$ hoặc $M(-6,-6a+b)$

M thuộc đường thẳng y = 3x + 4 => gọi M (m; 3m+4)
Khoảng cách từ M đến Ox bằng |3m + 4|
theo đề bài => |3m+4| = 2
<=> 3m + 4 = 2 hoặc 3m + 4 = -2
+) 3m + 4 = 2 <=> m = -2/3
+) 3m + 4 = -2 => m = -2
Vậy M (-2/3; 2); M (-2; -2)

\(a,PTHDGD:2x-1=-x+2\Leftrightarrow x=1\Leftrightarrow y=1\Leftrightarrow M\left(1;1\right)\\ b,\text{Gọi đt của }\left(d\right)\text{ là }y=ax+b\left(a\ne0\right)\\ \Leftrightarrow\left\{{}\begin{matrix}a+b=1\\0a+b=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=4\end{matrix}\right.\Leftrightarrow\left(d\right):y=-3x+4\)

1. Giả sử hai đường thẳng cắt nhau tại điểm M(x0; y0) trên trục tung
=> x0 = 0 => Thay toạ độ của M vào 2 đường thẳng ta có: (d): y0 = m và (d'): y0 = 3 - 2m
Xét phương trình hoành độ giao điểm: m = 3 - 2m ⇔ 3m = 3 ⇔ m = 1
=> Với m = 1 thì 2 đường thẳng cắt nhau tại điểm trên trục tung
2. Với m = 1 => y0 = 1 => 2 đường thẳng cắt nhau tại điểm M(0; 1)

Điểm M có tung độ y = 1 nên hoành độ là
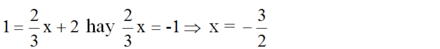
Điểm N có tung độ y = 1 nên hoành độ là