Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x(xe) là số xe ban đầu(Điều kiện: \(x\in Z^+\))
Ban đầu mỗi xe phải chở là: \(\dfrac{21}{x}\)(tấn)
Theo đề, ta có phương trình: \(\dfrac{21}{x-1}-\dfrac{1}{2}=\dfrac{21}{x}\)
\(\Leftrightarrow\dfrac{42x}{2x\left(x-1\right)}-\dfrac{x\left(x-1\right)}{2x\left(x-1\right)}=\dfrac{42\left(x-1\right)}{2x\left(x-1\right)}\)
Suy ra: \(42x-x^2+x=42x-42\)
\(\Leftrightarrow-x^2+41x-42x+42=0\)
\(\Leftrightarrow x^2-x-42=0\)
\(\Leftrightarrow x^2-7x+6x-42=0\)
\(\Leftrightarrow x\left(x-7\right)+6\left(x-7\right)=0\)
\(\Leftrightarrow\left(x-7\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-7=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=7\left(nhận\right)\\x=-6\left(loại\right)\end{matrix}\right.\)
Vậy: Lúc đầu có 7 xe

Gọi x (xe) là số xe mà công ty đã điều đến ban đầu (x>1).
Theo dự định, mỗi xe chở 21/x tấn hàng.
21/x tấn hàng của xe bị hỏng chia đều cho x-1 xe còn lại, mỗi xe được 0,5 tấn, ta có phương trình:
21/x:(x-1)=0,5 \(\Rightarrow\) \(\left\{{}\begin{matrix}x=7\left(nhận\right)\\x=-6\left(loại\right)\end{matrix}\right.\).
Vậy: ban đầu công ty đã điều đến kho hàng 7 xe.

Lời giải:
Giả sử số xe ban đầu dự định là $a$. ĐK: $a\in\mathbb{N}^*$.
Mỗi xe chở $\frac{90}{a}$ tấn hàng.
Theo bài ra ta có: 90=(a-2)(\frac{90}{a}+0,5)$
$\Leftrightarrow \frac{a}{2}-\frac{180}{a}-1=0$
$\Leftrightarrow a^2-2a-360=0$
$\Leftrightarrow (a-20)(a+18)=0$
Vì $a$ là số tự nhiên nên $a=20$

Gọi số xe đã điều khiển đến kho hàng lúc đầu là :x(xe,x thuộc u,x>1)
Nên số xe thực tế cho hàng là :x-1 xe;
Dự định mỗi xe chở 21/x tấn hàng
hàng
Thực tế mỗi xe phải chở thêm 0,5 tấn so với dự dih ban đầu nên :
21/x-1-21/x=0,5
Suy ra :x^2 - x -42 =0
<=>=7 (thỏa mãn x thuộc u ,x > 1) \(x_2\)= -6 loai
Vậy số xe lúc ban đầu là 7 xe

Gọi số xe ban đầu là x, x ∈ ℕ * (xe) nên số hàng theo kế hoạch mỗi xe chở là 24/x (tấn)
Số xe thực tế là x + 2 (xe) nên số hàng thực tế mỗi xe chở là 24/(x+2) (tấn)
Theo bài ra ta có phương trình:
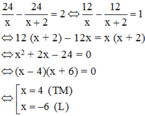
Vậy số xe ban đầu là 4 xe
Đáp án: A

Gọi số xe ban đầu của đội xe vận tải là \(x\left(x>2\right)\) (xe)
Số xe thực tế của đội xe vận tải là \(x-2\) (xe)
Số tấn hàng mỗi xe phải chở ban đầu là \(\dfrac{112}{x}\) (tấn hàng)
Số tấn hàng mỗi xe phải chở thực tế là \(\dfrac{112}{x-2}\) (tấn hàng)
Theo đề bài ta có phương trình: \(\dfrac{112}{x-2}-1=\dfrac{112}{x}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=16\left(\text{nhận}\right)\\x=-14\left(\text{loại}\right)\end{matrix}\right.\)
Vậy ban đầu đội xe vận tải có \(16\) xe.

Gọi số xe tài ban đầu tham gia chở hàng là a.
=> ban đầu mỗi xe phải chở số tấn hàng là: 15/a
Khi bớt đi 1 xe thì số xe còn lại là: a-1
Khi đó mỗi xe chở số tấn hàng là: 15/(a-1)
Theo bài ra ta có: 15/a + 0,5=15/(a-1)
<=> 15(a-1)+0,5a(a-1)=15a
<=> 15a-15+0,5a2-0,5a=15a
<=> a2 -a-30=0
<=> a=6 và a=-5 (chọn a=6)
Vậy số xe tải ban đầu là 6 xe
Đs: 6 xe
Hai giá sách có 450 cuốn. Nếu chuyển từ giá thứ nhất sang giá thứ hai 50 cuốn thì số sách ở giá thứ hai bằng 4/5 số sách giá thứ nhất .tìm số sách lúc đầu của mỗi giá

Gọi số xe dự định ban đầu là x (x nguyên dương)
Số hàng mỗi xe dự định phải chở: \(\frac{21}{x}\) (tấn)
Số hàng mỗi xe thực tế phải chở: \(\frac{21}{x-1}\)
Theo bài ra ta có pt:
\(\frac{21}{x-1}-\frac{21}{x}=\frac{1}{2}\)
\(\Leftrightarrow x\left(x-1\right)=42x-42\left(x-1\right)\)
\(\Leftrightarrow x^2-x-42=0\Rightarrow\left[{}\begin{matrix}x=7\\x=-6\left(l\right)\end{matrix}\right.\)