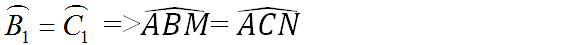Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.

A D E I B C M N
a) Xét \(\Delta ABD\) và \(\Delta ACE\) ,có :
AD = AE ( Tam giác ADE cân tại A )
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A )
BD = CE ( gt )
=> \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
=> AB = AC
=> \(\Delta ABC\) cân tại A
b) Xét \(\Delta BMD\) và \(\Delta CNE\) ,có :
BD = CE ( gt )
\(\widehat{BMD}=\widehat{CNE}=90^0\)
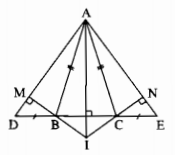
a) Xét ∆ADE cân tại A nên góc D = góc E
Xét ∆ABD và ∆ACE, ta có:
AD = AE (gt)
góc D = góc E (chứng minh trên)
DB = EC (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
Suy ra: AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.
b) Xét hai tam giác vuông BMD và CNE, ta có:
góc BMD=góc CNE=90o
BD = CE (gt)
góc D = góc E (chứng minh trên)
Suy ra: ∆BMD = ∆CNE (cạnh huyền, góc nhọn)
Suy ra: BM = CN (hai cạnh tương ứng)
c) Ta có: ∆BMD = ∆CNE (chứng minh trên)
Suy ra: góc DBM=góc ECN (hai góc tương ứng)
góc DBM=góc IBC (đối đỉnh)
góc ECN = góc ICB (đối đỉnh)
Suy ra: góc IBC=góc ICB hay ∆IBC cân tại I.
d) Xét ∆ABI và ∆ACI, ta có:
AB = AC (chứng minh trên)
IB = IC (vì ∆IBC cân tại I)
AI cạnh chung
Suy ra: ∆ABI = ∆ACI (c.c.c) ⇒ góc BAI=góc CAI (hai góc tương ứng)
Vậy AI là tia phân giác của góc BAC

a,xét tam giác ABD và tam giác ACE có:
AB=AC(gt)
vì \(\widehat{ABC}\)=\(\widehat{ACB}\)suy ra \(\widehat{ABD}\)=\(\widehat{ACE}\)
BD=CE(gt)
\(\Rightarrow\)\(\Delta\)ABD=\(\Delta\)ACE(c.g.c)
b,xét 2 tam giác vuông ADH và AEK có:
AD=AE(theo câu a)
\(\widehat{DAH}\)\(\widehat{EAK}\)(theo câu a)
\(\Rightarrow\)\(\Delta\)ADH=\(\Delta\)AEK(CH-GN)
\(\Rightarrow\)DH=EK
c,xét tam giác AHO và tam giác AKO có:
AH=AK(theo câu b)
AO cạnh chung
\(\Rightarrow\)\(\Delta\)AHO=\(\Delta\)AKO( cạnh góc vuông-cạnh huyền)
\(\Rightarrow\)\(\widehat{HAO}\)=\(\widehat{KAO}\)
\(\Rightarrow\)AO là phận giác của góc BAC
d,câu này dễ nên bn có thể tự làm tiếp nhé

1
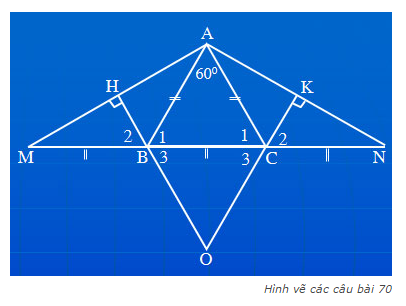
a) trước tiên chứng minh\(\widehat{ABM}=\widehat{ACN}\)
rồi mới chứng minh 2 tam giác ABM và ACN bằng nhau
suy ra AM = AN
b)Đầu tiên chứng minh\(\widehat{ABH}=\widehat{ACK}\)
rồi chứng minh hai tam giác ABH và ACK bằng nhau
suy ra BH = CK
c) vì hai tam giác ABH và ACK bằng nhau (cmt)
nên AH = AK
d) ta có \(\widehat{AMB}=\widehat{ACN}\)(hai tam giác ABH và ACK bằng nhau)
nên dễ cm \(\widehat{MBH}=\widehat{NCK}\)
còn lại tự cm
e) dễ cm tam giác ABC đều
vẽ \(BH\perp AC\)
nên BH vừa là đường cao; phân giác và trung tuyến
dễ cm \(\Delta BHC=\Delta NKC\)
nên \(\widehat{BCH}=\widehat{NCK}=60^0\)
từ đó dễ cm AMN cân và OBC dều

a) Tgiac ABC cân tại A => AB = AC và góc B = góc C
Xét tgiac ABD và ACE có:
+ AB = AC
+ góc B = C
+ BD = CE
=> tgiac ABD = ACE (cgc)
=> AD = AE
b) Xét tgiac BDF và CEG có:
+ BD = CE
+ góc B = góc C
+ góc BFD = CGE = 90 độ
=> tgiac BDF = CEG (ch-gn)
=> đpcm
c) Xét tgiac AFD và AGE có:
+ AD = AE (cmt)
+ góc FAD = GAE (vì tgiac ABD = ACE)
+ góc AFD = AGE = 90 độ
=> tgiac AFD = AGE (ch-gn)
=> góc ADF = AEG
=> góc EDH = DEH (hai góc đối đỉnh)
=> tgiac DEH cân tại H (đpcm)