Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

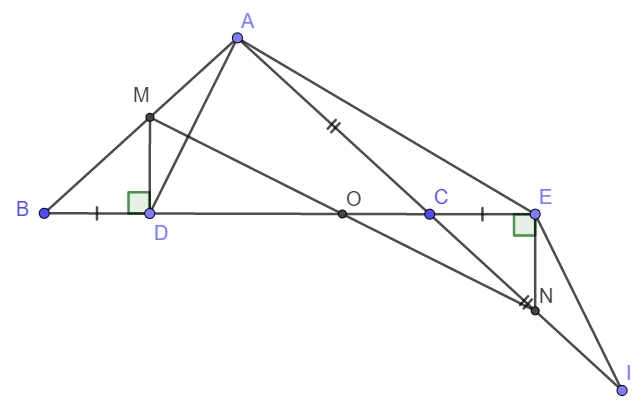
1)
+) Ta thấy \(\widehat{ECI}=\widehat{ACB}\) (Hai góc đối đỉnh)
Mà \(\widehat{ACB}=\widehat{ABC}\) (Tam giác ABC cân tại A)
nên \(\widehat{ECI}=\widehat{DBA}\)
Xét tam giác ABD và tam giác ICE có:
BD = CE (gt)
\(\widehat{DBA}=\widehat{ECI}\left(cmt\right)\)
CI = BA ( Cùng bằng AC)
\(\Rightarrow\Delta ABD=\Delta ICE\left(c-g-c\right)\)
+) Xét tam giác AEI, theo bất đẳng thức trong tam giác, ta có:
AI > AE + EI
Lại có do \(\Delta ABD=\Delta ICE\Rightarrow AD=IE\)
Vậy nên ta có AI > AE + AD \(\Rightarrow2AC>AD+AE\Rightarrow AB+AC>AD+AE\)
2) Do \(\Delta ABD=\Delta ICE\Rightarrow\widehat{MBD}=\widehat{NCE}\)
Vậy thì ta thấy ngay \(\Delta BDM=\Delta CEN\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow BM=CN\)
3) Ta thấy AB + AC = AM + MB + AC = AM + CN + AC = AM + AN
Ta cần chứng minh BC < MN.
Do BD = EC nên AC = DE
Xét tam giác vuông MDO ta có DO < MO (Quan hệ đường vuông góc, đường xiên)
Ta cũng có OE < ON
Vậy nên DE < MN hay BC < MN
Từ đó: AB + AC + BC < AM + AN + MN
Hay \(P_{AMN}>P_{ABC}\)

1. a) \(2009-\left|x-2009\right|=x\)
\(\Rightarrow\left|x-2009\right|=2009-x\)
\(\Rightarrow\left|x-2009\right|=-\left(x-2009\right)\)
\(\Rightarrow x-2009\le0\)
\(\Rightarrow x\le2009\)
Vậy \(x\le2009.\)
b) Ta có: \(\left[{}\begin{matrix}\left(2x-1\right)^{2008}\ge0\forall x\\\left(y-\dfrac{2}{5}\right)^{2008}\ge0\forall y\\\left|x+y-z\right|\ge0\forall x,y,z\end{matrix}\right.\) \(\Rightarrow\left(2x-1\right)^{2008}+\left(y-\dfrac{2}{5}\right)^{2008}+\left|x+y-z\right|\ge0\forall x,y,z\)
Dấu \("="\) xảy ra khi \(\left[{}\begin{matrix}\left(2x-1\right)^{2008}=0\\\left(y-\dfrac{2}{5}\right)^{2008}=0\\\left|x+y-z\right|=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{2}{5}\\z=\dfrac{9}{10}\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{2}{5}\\z=\dfrac{9}{10}\end{matrix}\right.\).
Bạn kia làm câu 1 rồi thì mình làm câu 2 nhé!
2. Ta có:\(\dfrac{3a-2b}{5}=\dfrac{2c-5a}{3}=\dfrac{5b-3c}{2}\)
\(\Rightarrow\dfrac{15a-10b}{25}=\dfrac{6c-15a}{9}=\dfrac{5b-3c}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{15a-10b}{25}=\dfrac{6c-15a}{9}=\dfrac{15a-10b+6c-15a}{25+9}\)=\(\dfrac{-10b+6c}{34}=\dfrac{-5b+3c}{17}\)
\(\Rightarrow\dfrac{-5b+3c}{17}=\dfrac{5b-3c}{2}\Rightarrow5b-3c=0\)
=> 5b=3c =>\(\left\{{}\begin{matrix}b=\dfrac{3}{5}c\\a=\dfrac{2}{5}c\end{matrix}\right.\)
=>\(\dfrac{3}{5}c+\dfrac{2}{5}c+c=-50\)
=> \(c\left(\dfrac{3}{5}+\dfrac{2}{5}+1\right)=-50\)
=> 2c = -50
=> c= -25
=>\(\left\{{}\begin{matrix}b=-25.\dfrac{3}{5}=-15\\a=-25.\dfrac{2}{5}=-10\end{matrix}\right.\)
Vậy a= -10; b= -15; c= -25

Ta luôn có :|x-2009|\(\ge\)0(1)
Mà :2009-|x-2009|=x nên 2009\(\ge\)x(2)
Vì (1)và(2) nên ta có x \(\in\){0;1;2;3;4;5;...;2009}

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath

Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath
bạn tìm ở link này sẽ có:
https://olm.vn/hoi-dap/question/1172749.html
Câu 3:
Giải:
Ta có: \(\frac{3a-2b}{5}=\frac{2c-5a}{3}=\frac{5b-3c}{2}\)
\(\Rightarrow\frac{15a-10b}{25}=\frac{6c-15a}{9}=\frac{10b-6c}{4}=\frac{15a-10b+6c-15a+10-6c}{25+9+4}=\frac{0}{25+9+4}=0\)
\(\Rightarrow\left\{\begin{matrix}\frac{15a-10b}{25}=0\\\frac{6c-15a}{9}=0\\\frac{10b-6c}{4}=0\end{matrix}\right.\Rightarrow\left\{\begin{matrix}15a-10b=0\\6c-15a=0\\10b-6c=0\end{matrix}\right.\Rightarrow\left\{\begin{matrix}15a=10b\\6c=15a\\10b=6c\end{matrix}\right.\)
\(\Rightarrow15a=10b=6c\)
\(\Rightarrow\frac{15a}{30}=\frac{10b}{30}=\frac{6c}{30}\)
\(\Rightarrow\frac{a}{2}=\frac{b}{3}=\frac{c}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{-50}{10}=-5\)
\(\Rightarrow\left\{\begin{matrix}a=-10\\b=-15\\c=-25\end{matrix}\right.\)
Vậy \(a=-10;b=-15;c=-25\)
3.Từ \(\dfrac{3a-2b}{5}=\dfrac{2c-5a}{3}=\dfrac{5b-3c}{2}\)
\(\Rightarrow\dfrac{15a-10b}{25}=\dfrac{6c-15a}{9}=\dfrac{10b-6c}{4}\)
Áp dụng tc dãy tỉ số bằng nhau ta có :
\(\dfrac{15a-10b}{25}=\dfrac{6c-15a}{9}=\dfrac{10b-6c}{4}=\dfrac{15a-10b+6c-15a+10b-6c}{25+4+9}=\dfrac{0}{25+4+9}=0\)
Áp dụng tc dãy tỉ số bằng nhau ta có :
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{10}=\dfrac{a+b+c}{4+6+10}=\dfrac{-50}{20}=\dfrac{-5}{2}\)
\(\Rightarrow\left\{{}\begin{matrix}a=-10\\b=-15\\c=-25\end{matrix}\right.\)