Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) Vì giá trị của biểu thức \(\frac{3x-2}{4}\) không nhỏ hơn giá trị của biểu thức \(\frac{3x+3}{6}\) nên \(\frac{3x-2}{4}\) \(\ge\) \(\frac{3x+3}{6}\)
TH1: \(\frac{3x-2}{4}\) = \(\frac{3x+3}{6}\)
=> (3x-2)6 = (3x+3)4
18x -12= 12x+12
=> x = 4
TH2: \(\frac{3x-2}{4}\) > \(\frac{3x+3}{6}\)
=> (3x-2)6 > (3x+3)4
18x-12> 12x+12
=> x \(\ge\) 5
b) Vì ( x+1)2 \(\ge\) 0; (x-1)2 \(\ge\) 0 mà (x+1) luôn lớn hơn (x-1) với mọi x nên không có giá trị của x thỏa mãn (x+1)2 nhỏ hơn (x-1)2
c) Phần c bạn cũng xét tương tự như phần a
TH1: \(\frac{2x-3}{35}+\frac{x\left(x-2\right)}{7}=\frac{x^2}{7}-\frac{2x-3}{5}\)
TH2: \(\frac{2x-3}{35}+\frac{x\left(x-2\right)}{7}<\frac{x^2}{7}-\frac{2x-3}{5}\)

ây bẹn ơi :<<<<
câu 3 ~
....
bạn vt sai chính tả ròi kìa :)) hé hé (cộng cả 2 vế của ...)
BĐT là bất đẳng thức mà, sai chỗ nào :VVVVV Miyuki Misaki

(Mk nghĩ bài 1 là 7m + 10 với 7n + 10, hoặc ngược lại, mk sẽ làm 2 TH)
1, TH1: Ta có: m < n
\(\Leftrightarrow\) 7m < 7n (nhân 2 vế của BĐT với 7)
\(\Leftrightarrow\) 7m + 10 < 7m + 10 (cộng 2 vế của BĐT với 10)
TH2: Ta có m < n
\(\Leftrightarrow\) -7m > -7n (nhân 2 vế của BĐT với -7)
\(\Leftrightarrow\) -7m + 10 > -7n + 10 (cộng 2 vế của BĐT với 10)
2, Biểu diễn bn tự làm nhé!
a, -4x + 8 \(\ge\) 0
\(\Leftrightarrow\) -4x \(\ge\) -8 (Cộng cả 2 vế của BĐT với -8)
\(\Leftrightarrow\) x \(\le\) 2 (Chia 2 vế của BĐT với -4)
b, 5 + 2x < 0
\(\Leftrightarrow\) 2x < -5 (cộng cả hai vế của BĐT với -5)
\(\Leftrightarrow\) x < \(\frac{-5}{2}\) (Chia cả hai vế của BĐT với 2)
3,
a, Ta có: 3x + 2 > 2(1 - 2x)
\(\Leftrightarrow\) 3x + 2 > 2 - 4x
\(\Leftrightarrow\) 3x > -4x (cộng cả vế cùa BĐT với -2)
\(\Leftrightarrow\) Vì 3 > -4 mà 3x > -4x
\(\Rightarrow\) x > 0 (Vì BĐT cùng chiều khi nhân x)
Vậy x > 0
b, Ta có: x - 3 < \(\frac{6-2x}{5}\)
\(\Leftrightarrow\) x - 3 < \(\frac{2\left(3-x\right)}{4}\)
\(\Leftrightarrow\) 4(x - 3) < 2(3 - x) (Nhân cả vế của BĐT với 4)
\(\Leftrightarrow\) 4(x - 3) < -2(x - 3)
Vì 4 > -2 mà 4(x - 3) < -2(x - 3)
\(\Rightarrow\) x - 3 < 0 (vì BĐT ngược chiều)
\(\Leftrightarrow\) x < 3 (Cộng cả hai vế của BĐT với 3)
Vậy x < 3
4, |-3x| = x + 6
\(\Leftrightarrow\left[{}\begin{matrix}-3x=x+6\Leftrightarrow-4x=6\Leftrightarrow x=\frac{-3}{2}\\-3x=-x-6\Leftrightarrow-2x=-6\Leftrightarrow x=3\end{matrix}\right.\)
Vậy S = {\(\frac{-3}{2}\); 3}
Chúc bn học tốt!!

a) Để giá trị biểu thức 5 – 2x là số dương
<=> 5 – 2x > 0
<=> -2x > -5 ( Chuyển vế và đổi dấu hạng tử 5 )
\(\Leftrightarrow x< \frac{5}{2}\)( Chia cả 2 vế cho -2 < 0 ; BPT đổi chiều )
Vậy : \(x< \frac{5}{2}\)
b) Để giá trị của biểu thức x + 3 nhỏ hơn giá trị biểu thức 4x - 5 thì:
x + 3 < 4x – 5
<=< x – 4x < -3 – 5 ( chuyển vế và đổi dấu các hạng tử 4x và 3 )
<=> -3x < -8
\(\Leftrightarrow x>\frac{8}{3}\)( Chia cả hai vế cho -3 < 0, BPT đổi chiều).
Vậy : \(x>\frac{8}{3}\)
c) Để giá trị của biểu thức 2x +1 không nhỏ hơn giá trị của biểu thức x + 3 thì:
2x + 1 ≥ x + 3
<=> 2x – x ≥ 3 – 1 (chuyển vế và đổi dấu các hạng tử 1 và x).
<=> x ≥ 2.
Vậy x ≥ 2.
d) Để giá trị của biểu thức x2 + 1 không lớn hơn giá trị của biểu thức (x - 2)2 thì:
x2 + 1 ≤ (x – 2)2
<=> x2 + 1 ≤ x2 – 4x + 4
<=> x2 – x2 + 4x ≤ 4 – 1 ( chuyển vế và đổi dấu hạng tử 1; x2 và – 4x).
<=> 4x ≤ 3
\(\Leftrightarrow x\le\frac{3}{4}\)( Chia cả 2 vế cho 4 > 0 )
Vậy : \(x\le\frac{3}{4}\)

Answer:
a) \(\frac{5x}{2x+2}+1=\frac{6}{x+1}\)
\(\Rightarrow\frac{5x}{2\left(x+1\right)}+\frac{2\left(x+1\right)}{2\left(x+1\right)}=\frac{12}{2\left(x+1\right)}\)
\(\Rightarrow5x+2x+2-12=0\)
\(\Rightarrow7x-10=0\)
\(\Rightarrow x=\frac{10}{7}\)
b) \(\frac{x^2-6}{x}=x+\frac{3}{2}\left(ĐK:x\ne0\right)\)
\(\Rightarrow x^2-6=x^2+\frac{3}{2}x\)
\(\Rightarrow\frac{3}{2}x=-6\)
\(\Rightarrow x=-4\)
c) \(\frac{3x-2}{4}\ge\frac{3x+3}{6}\)
\(\Rightarrow\frac{3\left(3x-2\right)-2\left(3x+3\right)}{12}\ge0\)
\(\Rightarrow9x-6-6x-6\ge0\)
\(\Rightarrow3x-12\ge0\)
\(\Rightarrow x\ge4\)
d) \(\left(x+1\right)^2< \left(x-1\right)^2\)
\(\Rightarrow x^2+2x+1< x^2-2x+1\)
\(\Rightarrow4x< 0\)
\(\Rightarrow x< 0\)
e) \(\frac{2x-3}{35}+\frac{x\left(x-2\right)}{7}\le\frac{x^2}{7}-\frac{2x-3}{5}\)
\(\Rightarrow\frac{2x-3+5\left(x^2-2x\right)}{35}\le\frac{5x^2-7\left(2x-3\right)}{35}\)
\(\Rightarrow2x-3+5x^2-10x\le5x^2-14x+21\)
\(\Rightarrow6x\le24\)
\(\Rightarrow x\le4\)
f) \(\frac{3x-2}{4}\le\frac{3x+3}{6}\)
\(\Rightarrow\frac{3\left(3x-2\right)-2\left(3x+3\right)}{12}\le0\)
\(\Rightarrow9x-6-6x-6\le0\)
\(\Rightarrow3x\le12\)
\(\Rightarrow x\le4\)

1:
a: 2x-3=5
=>2x=8
=>x=4
b: (x+2)(3x-15)=0
=>(x-5)(x+2)=0
=>x=5 hoặc x=-2
2:
b: 3x-4<5x-6
=>-2x<-2
=>x>1

a: Để \(\dfrac{3x-2}{4}\) không nhỏ hơn \(\dfrac{3x+3}{6}\) thì \(\dfrac{3x-2}{4}>=\dfrac{3x+3}{6}\)
=>\(\dfrac{6\left(3x-2\right)}{24}>=\dfrac{4\left(3x+3\right)}{24}\)
=>18x-12>=12x+12
=>6x>=24
=>x>=4
b: Để \(\left(x+1\right)^2\) nhỏ hơn \(\left(x-1\right)^2\) thì \(\left(x+1\right)^2< \left(x-1\right)^2\)
=>\(x^2+2x+1< x^2-2x+1\)
=>4x<0
=>x<0
c: Để \(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}\) không lớn hơn \(\dfrac{x^2}{7}-\dfrac{2x-3}{5}\) thì
\(\dfrac{2x-3}{35}+\dfrac{x\left(x-2\right)}{7}< =\dfrac{x^2}{7}-\dfrac{2x-3}{5}\)
=>\(\dfrac{2x-3+5x\left(x-2\right)}{35}< =\dfrac{5x^2-7\cdot\left(2x-3\right)}{35}\)
=>\(2x-3+5x^2-10x< =5x^2-14x+21\)
=>-8x-3<=-14x+21
=>6x<=24
=>x<=4
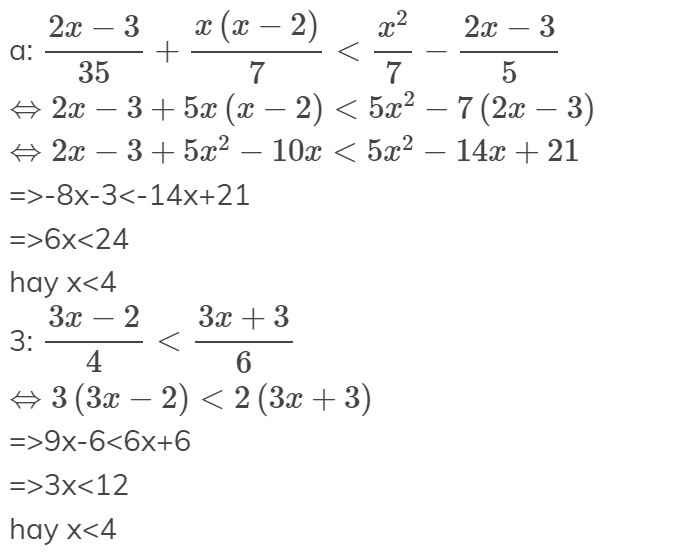
Bài 1:
Ta có: m>n
\(\Leftrightarrow8m>8n\)
\(\Leftrightarrow8m-2>8n-2\)
Bài 3:
a) Ta có: 2-5x<3(2-x)
\(\Leftrightarrow2-5x< 6-3x\)
\(\Leftrightarrow2-5x-6+3x< 0\)
\(\Leftrightarrow-4-2x< 0\)
\(\Leftrightarrow2x< -4\)
hay x<-2
b) Ta có: \(\frac{5x-2}{3}\ge x+1\)
\(\Leftrightarrow\frac{5x-2}{3}-x-1\ge0\)
\(\Leftrightarrow\frac{5x-2}{3}-\frac{3x}{3}-\frac{3}{3}\ge0\)
\(\Leftrightarrow5x-2-3x-3\ge0\)
\(\Leftrightarrow2x-5\ge0\)
\(\Leftrightarrow2x\ge5\)
hay \(x\ge\frac{5}{2}\)
Bài 4:
Ta có: |x+5|=3x-2
\(\Leftrightarrow\left[{}\begin{matrix}x+5=3x-2\\x+5=2-3x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+5-3x+2=0\\x+5-2+3x=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}-2x+7=0\\4x+3=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}-2x=-7\\4x=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\frac{7}{2}\\x=\frac{-3}{4}\end{matrix}\right.\)
Vậy: \(S=\left\{\frac{7}{2};\frac{-3}{4}\right\}\)
1. Cho m > n, hãy so sánh 8m - 2 với 8n - 2
Ta có : \(m>n\)
\(\Rightarrow8m>8n\)
\(\Rightarrow8m-2>8n-2\)