Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a . Điện trở tương đương của đoạn mạch AB và hiệu điện thế giữa hai đầu mỗi điện trở.
– Điện trở tương đương:
R = R1 + R2 = 8 +4 = 12 (Ω)
– Cường độ dòng điện trong mạch
I = = = 2(A)
– Hiệu điện thế giữa hai đầu R1, R2:
U1 = I1R1 = 2.8 = 16(V)
U2 = I2R2 = 2.4 = 8(V)
b.
Công suất điện tiêu thụ: (công thức đúng 0,25đ)
P = U.I = 24 . 2 = 48 (W)
c.
Chiều dài của dây dẫn R2: (công thức đúng 0,25đ)
![]()
d.
Điện trở của biến trở:
– Cường độ dòng điện qua R1:
P1 = I12R1
![]() = 0,25(A) ⇒ I1 = 0,5(A)
= 0,25(A) ⇒ I1 = 0,5(A)
-Điện trở toàn mạch:
![]()
– Điện trở của biến trở:
Rb = R – R12 = 48 – 12 = 36 (Ω)
cho mk hỏi thêm ý này nha
Để công suất tiêu thụ của điện trở R1 là cực đại thì biến trở phỉa có giá trị là bao nhiêu ?

1. a. Theo ht 4' trg đm //, ta có: Rtđ= (R1.R2)/(R1+R2)= (3.6)/(3+6)=2 ôm
b.Theo ĐL ôm, ta có: I= U/Rtđ=24/2=12 A
I1=U/R1=24/3=8 ôm
I2=U/R2=24/6=4 ôm
2. a. Theo ht 4' trg đm //, ta có: Rtđ=(R1.R2.R3)/(R1+R2+R3)= (6.12.4)/(6+12+4)=13,09 ôm
b. Áp dụng ĐL Ôm, ta có: U=I.R=3.13,09=39,27 V
c. Theo ĐL Ôm, ta có:
I1=U/R1=39,27/6=6.545 A
I2=U/R2=39,27/12=3,2725 A
I3=U/R3=39,27/4=9.8175 A

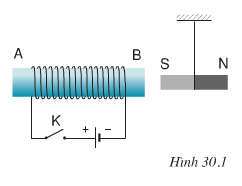
a) Thanh nam châm bị hút vào ống dây.
b) Lúc đầu nam châm bị đẩy ra xa, sau đó xoay đi và khi cực Bắc của nam châm hướng về phía đầu B của ống dây thì nam châm lại bị hút vào ống dây.
a.Treo thanh nam châm gần một ống dây (hình 30.1 SGK). Đóng mạch điện
\(\Rightarrow\) Nam châm bị hút vào ống dây
b. Lúc đầu nam châm bị đẩy ra xa, sau đó nó xoay đi và khi cực Bắc của nam châm hướng về phía đầu B của ống dây thì nam châm bị hút vào ống dây

\(MCD:\left(R2//R3\right)ntR1\)
\(\rightarrow R=\dfrac{R2\cdot R3}{R2+R3}+R1=\dfrac{10\cdot12}{10+12}+10=\dfrac{170}{11}\Omega\)
\(I=I1=I23=U:R=24:\dfrac{170}{11}=\dfrac{132}{85}A\)
\(\rightarrow U1=I1\cdot R1=\dfrac{132}{85}\cdot10=\dfrac{264}{17}V\)
\(\rightarrow U23=U2=U3=U-U1=24-\dfrac{264}{17}=\dfrac{144}{17}V\)
\(\rightarrow\left\{{}\begin{matrix}I2=U2:R2=\dfrac{144}{17}:10=\dfrac{72}{85}A\\I3=U3:R3=\dfrac{144}{17}:12=\dfrac{12}{17}A\end{matrix}\right.\)

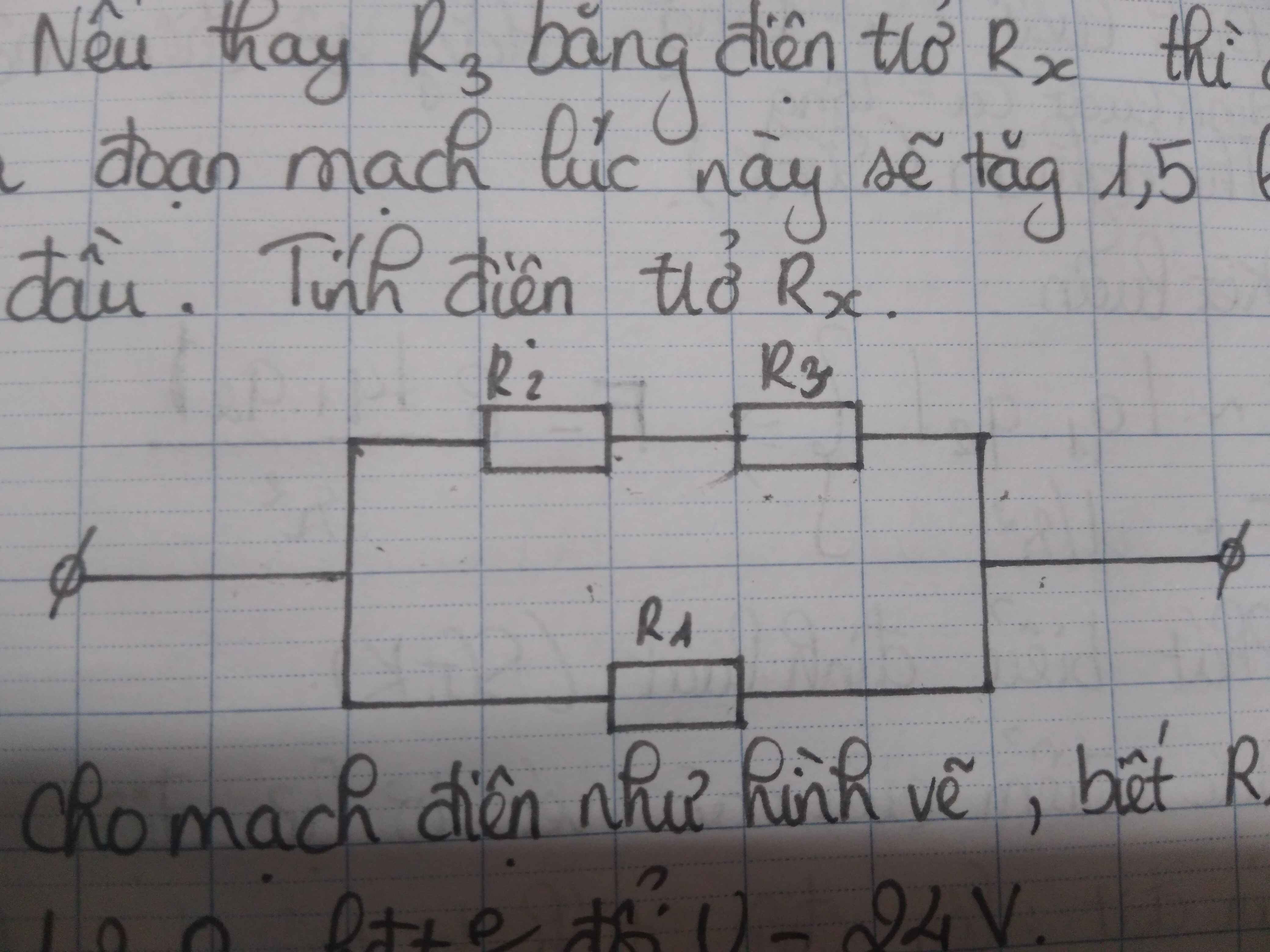
\(\Rightarrow\left\{{}\begin{matrix}a,R1//\left(R2ntR3\right)\Rightarrow Rtd=\dfrac{R1\left(R2+R3\right)}{R1+R2+R3}=6\Omega\\b,\Rightarrow\left\{{}\begin{matrix}U=U1=U23=24V\Rightarrow I1=\dfrac{U1}{R1}=\dfrac{8}{3}A\\I2=I3=\dfrac{U23}{R2+R3}=\dfrac{4}{3}A\\U2=I2.R2=8V\\U3=U-U2=16V\end{matrix}\right.\\c,R1//\left(R2ntRx\right)\Rightarrow Im=1,5.\dfrac{24}{6}=6A\\\Rightarrow Rtd=\dfrac{R1\left(R2+Rx\right)}{R1+R2+Rx}=\dfrac{9\left(6+Rx\right)}{15+Rx}=\dfrac{24}{Im}=4\left(\Omega\right)\Rightarrow Rx=1,2\Omega\end{matrix}\right.\)
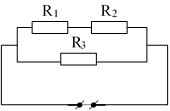

a) \(R_{12}=R_1+R_2=1+2=3\left(\Omega\right)\)
\(R_{tđ}=\dfrac{R_{12}.R_3}{R_{12}+R_3}=\dfrac{3.3}{3+3}=1,5\left(\Omega\right)\)
b) \(U=U_{12}=U_3=6V\)
\(I_{12}=I_1=I_2=\dfrac{U_{12}}{R_{12}}=\dfrac{6}{3}=2\left(A\right)\)
\(I_3=\dfrac{U_3}{R_3}=\dfrac{6}{3}=2\left(A\right)\)
c) \(P=\dfrac{U^2}{R}=\dfrac{6^2}{1,5}=24\left(W\right)\)