Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác BMDN có
BN//DM
BN=DM
Do đó: BMDN là hình bình hành
Suy ra: BM//DN
b: Ta có: BMDN là hình bình hành
nên BD cắt MN tại trung điểm của mỗi đường(1)
Ta có: ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1) và (2) suy ra BD,MN,AC đồng quy

Xét tam giác ADM và tam giác CBN có:
AD = CN (ABCD là hình bình hành)
ADM = CBN (2 góc so le trong, AB // CB)
DM = BN (gt)
=> Tam giác ADM = Tam giác CBN (c.g.c)
=> AM = CN (2 cạnh tương ứng)
AMD = CNB (2 góc tương ứng) => 1800 - AMD = 1800 - CNB => AMN = CNM mà 2 góc này ở vị trí so le trong => AM // CN
=> AMCN là hình bình hành
=> AMCN là hình thoi
<=> AC _I_ BD
<=> ABCD là hình thoi

A B C D 5cm 1 1 2 1
Xét \(\Delta ABD\) có :
\(\begin{cases}AB=AD\\\widehat{A}=90^0\end{cases}\)=> \(\Delta ABD\) vuông cân tại A
\(\Rightarrow\begin{cases}\widehat{B_1}=\widehat{D_1}=45^0\\AB^2+AD^2=BD^2\end{cases}\)
\(\Rightarrow\begin{cases}\widehat{B_1}=\widehat{D_1}=45^0\\5^2+5^2=BD^2\end{cases}\)
\(\Rightarrow\begin{cases}\widehat{B_1}=\widehat{D_1}=45^0\\50=BD^2\end{cases}\)
\(\Rightarrow\begin{cases}\widehat{B_1}=\widehat{D_1}=45^0\\BD=5\sqrt{2}\end{cases}\)
Mà \(\widehat{D_2}+\widehat{D_1}=90^0\)
\(\Rightarrow\widehat{D_2}=45^0\)
\(\Rightarrow\widehat{ABC}=135^0\)
Mặt khác :\(\widehat{C_1}+\widehat{ABC}=180^0\)
\(\Rightarrow\widehat{C_1}=45^0\)
\(\Rightarrow\Delta BDC\) vuông cân tại B
\(\Rightarrow BD=BC=5\sqrt{2}\)
\(\Rightarrow\left(5\sqrt{2}\right)^2+\left(5\sqrt{2}\right)^2=CD^2\)
\(\Rightarrow50+50=CD^2\)
\(\Rightarrow CD=10\)
\(\Rightarrow S_{ABCD}=\frac{\left(10+5\right).5}{2}=\frac{15.5}{2}=\frac{75}{2}\left(cm^2\right)\)
Vậy diện tích ABCD là \(\frac{75}{2}cm^2\)
Ta có AB = AD => Góc ABD = góc ADB = 45 độ.
Mà BDC = ABD (so le trong) và ADB = BCD ( cùng phụ góc BDC)
=> Tam giác BDC là tam giác vuông cân tại B
Xét tam giác ABD, áp dụng Pytago ta được BD = 5 căn 2. cm
=> CD = 10 cm.
=> Diện tích hình thang ABCD là 37,5 cm2
(Bạn tự vẽ hình nhé. sai chỗ nào mong bạn thông cảm :)))

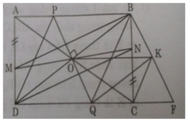
b) O là trung điểm của BD mà ABCD là hình chữ nhật nên đường chéo thứ hai AC phải qua O.
Lại có tứ giác BMDN là hình bình hành nên MN phải đi qua trung điểm O của BD.
Vậy AC, BD, MN đồng quy tại O.
a: Xét tứ giác BMDN có
BN//DM
BN=DM
Do đó: BMDN là hình bình hành
Suy ra: BM//DN
b: Ta có: ABCD là hình chữ nhật
nên AC cắt BD tại trung điểm của mỗi đường
hay O là trung điểm chung của AC và BD(1)
Ta có: BMDN là hình bình hành
nên BD cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của BD
nên O là trung điểm của MN(2)
Từ (1) và (2) suy ra AC,BD,MN đồng quy