Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi gặp dạng này, ý tưởng là sẽ tìm 1 hàm u(x) sao cho:
\(\int\limits^b_a\left[f'\left(x\right)-u\left(x\right)\right]^2dx=0\) (1)
\(\Rightarrow f'\left(x\right)-u\left(x\right)=0\Rightarrow f'\left(x\right)=u\left(x\right)\)
Khai triển (1), đề cho sẵn \(\left[f'\left(x\right)\right]^2\) nên đại lượng \(2u\left(x\right).f'\left(x\right)\) và hàm \(u\left(x\right)\) sẽ được suy ra từ việc tích phân từng phần \(\int\limits f\left(x\right)dx\). Cụ thể:
Xét \(I=\dfrac{2}{3}=\int\limits^2_0f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I=x.f\left(x\right)|^2_0-\int\limits^2_0xf'\left(x\right)dx=2-\int\limits^2_0xf'\left(x\right)dx\)
\(\Rightarrow\int\limits^2_0xf'\left(x\right)dx=2-\dfrac{2}{3}=\dfrac{4}{3}\) (2)
(Vậy đến đây hàm \(u\left(x\right)\) được xác định là dạng \(u\left(x\right)=k.x\)
Để tìm cụ thể giá trị k:
Từ (1) ta suy luận tiếp:
\(\int\limits^2_0\left[f'\left(x\right)-kx\right]^2dx=0\Leftrightarrow\int\limits^2_0\left[f'\left(x\right)\right]^2-2k\int\limits^2_0x.f'\left(x\right)dx+\int\limits^2_0k^2x^2dx=0\)
\(\Leftrightarrow\dfrac{2}{3}-2k.\dfrac{4}{3}+\dfrac{8}{3}k^2=0\) do \(\int\limits^2_0x^2dx=\dfrac{8}{3}\)
\(\Rightarrow k=\dfrac{1}{2}\)
\(\Rightarrow u\left(x\right)=\dfrac{1}{2}x\) coi như xong bài toán)
Do đó ta có:
\(\int\limits^2_0\left[f'\left(x\right)\right]^2-\int\limits^2_0xf'\left(x\right)+\dfrac{1}{4}\int\limits^2_0x^2dx=\dfrac{2}{3}-\dfrac{4}{3}+\dfrac{1}{4}.\dfrac{8}{3}=0\)
\(\Rightarrow\int\limits^2_0\left[f'\left(x\right)-\dfrac{1}{2}x\right]^2dx=0\)
\(\Rightarrow f'\left(x\right)-\dfrac{1}{2}x=0\)
\(\Rightarrow f'\left(x\right)=\dfrac{1}{2}x\Rightarrow f\left(x\right)=\dfrac{1}{4}x^2+C\)
Thay \(x=2\Rightarrow1=1+C\Rightarrow C=0\)
\(\Rightarrow f\left(x\right)=\dfrac{1}{4}x^2\)

2a. Đề sai, nhìn biểu thức \(\dfrac{f'\left(x\right)}{f'\left(x\right)}dx\) là thấy
2b. Đồ thị hàm số không cắt Ox trên \(\left(0;1\right)\) nên diện tích cần tìm:
\(S=\int\limits^1_0\left(x^4-5x^2+4\right)dx=\dfrac{38}{15}\)
3a. Phương trình (P) theo đoạn chắn:
\(\dfrac{x}{4}+\dfrac{y}{-1}+\dfrac{z}{-2}=1\)
3b. Câu này đề sai, đề cho mặt phẳng (Q) rồi thì sao lại còn viết pt mặt phẳng (Q) nữa?
sorry thầy em xin sửa lại câu 3 b là
b) trong không gian Oxyz cho mặt phẳng (Q): 3x-y-2z+1=0.Viết phương trình mặt phẳng (P) song song với mặt phẳng (Q) và đi qua điểm M(0;0;1)

Chọn đáp án D
![]()
![]()
![]()
![]()
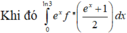
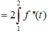

![]()
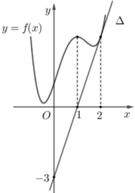
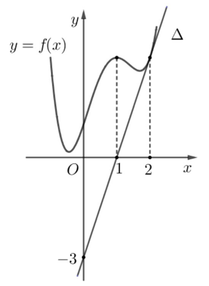
Do hàm số đạt cực đại tại điểm x=1⇒ f′(1) = 0 và đường thẳng Δ qua hai điểm (0;−3);(1;0) nên có phương trình y=3x−3.
Vì Δ là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 ⇒ f ' ( 2 ) = k △ =3
Vậy
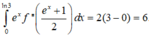

Đặt \(2x+2=u\Rightarrow2xdx=du\Rightarrow dx=\dfrac{1}{2}du\)
\(\left\{{}\begin{matrix}x=0\Rightarrow u=2\\x=2\Rightarrow u=6\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^6_2f\left(u\right).\dfrac{1}{2}du=\dfrac{1}{2}\int\limits^6_2f\left(u\right)du=\dfrac{1}{2}\int\limits^6_2f\left(x\right)dx=\dfrac{1}{2}.6=3\)

Xét \(I=\int\limits^1_0x.f\left(3x\right)dx\)
Đặt \(3x=u\Rightarrow dx=\dfrac{1}{3}du\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow u=0\\x=1\Rightarrow u=3\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{9}\int\limits^3_0u.f\left(u\right)du=\dfrac{1}{9}\int\limits^3_0x.f\left(x\right)dx=1\)
\(\Rightarrow J=\int\limits^3_0x.f\left(x\right)dx=9\)
Xét J, đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=x.dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=\dfrac{x^2}{2}\end{matrix}\right.\)
\(\Rightarrow J=\dfrac{x^2}{2}.f\left(x\right)|^3_0-\dfrac{1}{2}\int\limits^3_0x^2.f'\left(x\right)dx=\dfrac{9}{2}-\dfrac{1}{2}\int\limits^3_0x^2.f'\left(x\right)dx\)
\(\Rightarrow\int\limits^3_0x^2.f'\left(x\right)dx=9-2J=-9\)

Câu 4:
Do \(f\left(x\right)\) là hàm chẵn \(\Rightarrow f\left(x\right)=f\left(-x\right)\) \(\forall x\)
Xét tích phân:
\(I=\int\limits^0_{-5}f\left(x\right)dx\)
Đặt \(x=-t\Rightarrow dx=-dt\) ; \(\left\{{}\begin{matrix}x=-5\Rightarrow t=5\\x=0\Rightarrow t=0\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^0_5f\left(-t\right)\left(-dt\right)=\int\limits^5_0f\left(-t\right)dt=\int\limits^5_0f\left(t\right)dt=\int\limits^5_0f\left(x\right)dx\)
Vậy:
\(\frac{3}{2}\int\limits^5_{-5}f\left(x\right)dx=\frac{3}{2}\left(\int\limits^0_{-5}f\left(x\right)dx+\int\limits^5_0f\left(x\right)dx\right)=\frac{3}{2}.2\int\limits^5_0f\left(x\right)dx=3.5=15\)
Câu 1:
Gọi O là tâm đáy , G là trọng tâm tam giác đều SAB
Qua O kẻ đường thẳng d vuông góc mặt phẳng (ABCD) (đường thẳng này song song SG)
Trong mặt phẳng (SGO) hay mở rộng là (SHO) với H là trung điểm BC, qua G kẻ đường thẳng song song OH cắt d tại T \(\Rightarrow T\) là tâm mặt cầu ngoại tiếp tứ diện
Ta có \(OT=GH=\frac{1}{3}SH=\frac{1}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{6}\)
\(OB=\frac{1}{2}BD=\frac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{TBD}=\frac{OT}{OB}=\frac{\sqrt{6}}{6}\Rightarrow\widehat{TBD}\approx22^012'\)
Câu 2:
Phương trình đoạn chắn của mặt phẳng (ABC): \(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1\)
Do \(\frac{1}{a}+\frac{2}{b}+\frac{3}{c}=7\Leftrightarrow\frac{\frac{1}{7}}{a}+\frac{\frac{2}{7}}{b}+\frac{\frac{3}{7}}{c}=1\)
\(\Rightarrow\left(ABC\right)\) luôn đi qua điểm cố định \(D\left(\frac{1}{7};\frac{2}{7};\frac{3}{7}\right)\)
Gọi \(I\left(1;2;3\right)\) là tâm mặt cầu
\(\Rightarrow ID^2=\left(1-\frac{1}{7}\right)^2+\left(2-\frac{2}{7}\right)^2+\left(3-\frac{3}{7}\right)^2=\frac{72}{7}=R^2\)
\(\Rightarrow D\) chính là tiếp điểm của mặt cầu (S) và mặt phẳng (ABC)
\(\Rightarrow ID\perp\left(ABC\right)\) , mà \(\overrightarrow{DI}=\left(\frac{6}{7};\frac{12}{7};\frac{18}{7}\right)=\frac{6}{7}\left(1;2;3\right)\)
\(\Rightarrow\left(ABC\right)\) nhận \(\overrightarrow{n}=\left(1;2;3\right)\) là 1 vtpt
Phương trình (ABC):
\(1\left(x-\frac{1}{7}\right)+2\left(y-\frac{2}{7}\right)+3\left(z-\frac{3}{7}\right)=0\)
\(\Rightarrow\)Giao điểm của (ABC) và các trục tọa độ: \(A\left(2;0;0\right)\) ;\(B\left(0;1;0\right)\); \(C\left(0;0;\frac{2}{3}\right)\)
Thể tích tứ diện: \(V=\frac{1}{3}.1.2.\frac{2}{3}=\frac{4}{9}\)
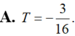
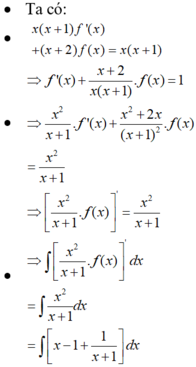
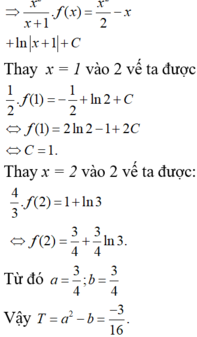
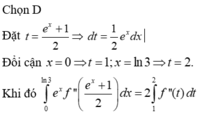
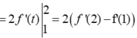

Câu 1:
\(\left(x+2\right)f\left(x\right)+x\left(x+1\right)f'\left(x\right)=x\left(x+1\right)\)
\(\Leftrightarrow x\left(x+2\right)f\left(x\right)+x^2\left(x+1\right)f'\left(x\right)=x^2\left(x+1\right)\)
\(\Leftrightarrow\frac{x\left(x+2\right)}{\left(x+1\right)^2}f\left(x\right)+\frac{x^2}{x+1}f'\left(x\right)=\frac{x^2}{x+1}\)
\(\Leftrightarrow\left(\frac{x^2}{x+1}f\left(x\right)\right)'=\frac{x^2}{x+1}=x-1+\frac{1}{x+1}\)
Lấy nguyên hàm 2 vế:
\(\Leftrightarrow\frac{x^2}{x+1}.f\left(x\right)=\frac{x^2}{2}-x+ln\left|x+1\right|+C\)
Thay \(x=1\Rightarrow ln2+\frac{1}{2}=\frac{1}{2}-1+ln2+C\Rightarrow C=1\)
\(\Rightarrow\frac{x^2}{x+1}f\left(x\right)=\frac{x^2}{2}-x+ln\left|x+1\right|+1\)
Thay \(x=2\Rightarrow\frac{4}{3}f\left(2\right)=ln3+1\Rightarrow f\left(2\right)=\frac{3}{4}ln+\frac{3}{4}\Rightarrow T=-\frac{3}{16}\)
Câu 2:
\(I_1=\int\limits^2_0f\left(x\right)dx\)
Đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=x\end{matrix}\right.\)
\(\Rightarrow I_1=x.f\left(x\right)|^2_0-\int\limits^2_0x.f'\left(x\right)dx=2-\int\limits^2_0x.f'\left(x\right)dx\)
Mà \(I_1=2\)\(\Rightarrow I_2=\int\limits^2_0x.f'\left(x\right)dx=-2\)
Đặt \(2x=t\Rightarrow x=\frac{t}{2}\Rightarrow dx=\frac{1}{2}dt\) ; \(\left\{{}\begin{matrix}x=0\Rightarrow t=0\\x=2\Rightarrow t=4\end{matrix}\right.\)
\(\Rightarrow I_2=\int\limits^4_0\frac{t}{2}f'\left(\frac{t}{2}\right).\frac{1}{2}dt=\frac{1}{4}\int\limits^4_0t.f'\left(\frac{t}{2}\right)dt=-2\)
\(\Rightarrow\int\limits^4_0t.f'\left(\frac{t}{2}\right)dt=-8\) hay \(\int\limits^4_0x.f'\left(\frac{x}{2}\right)dx=-8\)