Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Rightarrow\left\{{}\begin{matrix}I1=\dfrac{18}{R1}\\I2=\dfrac{18}{R2}\end{matrix}\right.\)\(\Rightarrow I2=I1+3\Rightarrow\dfrac{18}{R2}=\dfrac{18}{2R2}+3\Rightarrow\left\{{}\begin{matrix}R2=3\Omega\\R1=6\Omega\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}I1=\dfrac{18}{6}=3A\\I2=\dfrac{18}{3}=6A\end{matrix}\right.\)

Ta có:
\(I_1=\dfrac{U}{R_1}=\dfrac{16}{R_1}\)
\(I_2=\dfrac{U}{R_2}=\dfrac{16}{R_2}\)
Mà theo bài cho:
\(R_1=4R_2\Rightarrow R_2=\dfrac{R_1}{4}\)
\(I_2=I_1+6\) \(\Rightarrow I_1+6=\dfrac{4.16}{R_1}\)
\(\Rightarrow\dfrac{16}{R_1}+6=\dfrac{64}{R_1}\)
\(\Rightarrow\dfrac{48}{R_1}=6\Rightarrow R_1=8\left(\Omega\right)\)
\(\Rightarrow R_2=2\left(\Omega\right)\)
Cường độ dòng điện qua 2 điện trở lần lượt là:
\(I_1=\dfrac{16}{8}=2\) (A)
\(I_2=\dfrac{16}{2}=8\) (A)

\(I_1=\dfrac{U}{R_1}=\dfrac{16}{R_1}\left(A\right)\)
\(I_2=\dfrac{U}{R_2}=\dfrac{16}{R_2}\left(A\right)\)
\(TC:\)
\(R_1=3R_2\)
\(I_2=I_1+8\)
\(\Leftrightarrow\dfrac{16}{R_2}=\dfrac{16}{R_1}+8\)
\(\Leftrightarrow\dfrac{16}{R_2}=\dfrac{16}{3R_2}+8\)
\(\Leftrightarrow R_2=\dfrac{4}{3}\)Ω
\(R_1=3R_2=3\cdot\dfrac{4}{3}=4\)Ω
\(I_1=\dfrac{16}{4}=4\left(A\right)\)
\(I_2=\dfrac{16}{\dfrac{4}{3}}=12\left(A\right)\)
\(I1=\dfrac{16}{R1}\), \(I2=\dfrac{16}{R2}\)
mà \(R1=3R2=>I1=\dfrac{16}{3R2}\)(1)\(I2=I1+8=>I1+8=\dfrac{16}{R2}=>I1=\dfrac{16}{R2}-8\)(2)
(1)(2)=>\(\dfrac{16}{3R2}=\dfrac{16}{R2}-8< =>R2=\dfrac{4}{3}\)ôm
\(=>R1=4\) ôm
\(=>I1=\dfrac{16}{4}=4\left(A\right)\), \(I2=16:\dfrac{4}{3}=12A\)

R 1 nối tiếp R 2 nên điện trở tương đương của mạch lúc này là:
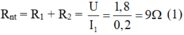
R 1 song song với R 2 nên điện trở tương đương của mạch lúc này là:
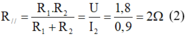
Lấy (1) nhân với (2) theo vế ta được
R
1
.
R
2
= 18 → 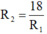 (3)
(3)
Thay (3) vào (1), ta được: R 12 - 9 R 1 + 18 = 0
Giải phương trình, ta có: R 1 = 3Ω; R 2 = 6Ω hay R 1 = 6Ω; R 2 = 3Ω

Bài giải :
Vì R1//R2 nên :
\(U=U_1=U_2\)
\(\Rightarrow\left\{{}\begin{matrix}I_1=\dfrac{U}{R_1}\\I_2=\dfrac{U}{R_2}\end{matrix}\right.\)
\(\Rightarrow\dfrac{I_1}{I_2}=\dfrac{R_2}{R_1}\)
Mà : \(R_1=5R_2=>\dfrac{R_1}{R_2}=5\)
\(=>\dfrac{I_2}{I_1}=\dfrac{R_1}{R_2}=5\)
\(=>I_2=5I_1\left(1\right)\)
Và : \(I_2=24-I_1\left(2\right)\)
Ta thay 5I1 ở (1) vào I2 ở (2) có :
\(5I_1=24-I_1\)
\(=>I_1=\dfrac{24}{5+1}=\dfrac{24}{6}=4\left(A\right)\)
\(I_2=5I_1=5.4=20\left(A\right)\)
Điện trở R1 bằng :
\(R_1=\dfrac{U}{I_1}=\dfrac{U}{4}\left(\Omega\right)\)
Điện trở R2 là :
\(R_2=\dfrac{U}{I_2}=\dfrac{U}{20}\left(\Omega\right)\)
GIẢI :
Ta có : R1//R2 nên :
U=U1=U2
Cường độ dòng điện qua điện trở R1 là :
\(\text{I1=U/R1}\)
Cường độ dòng điện qua điện trở R2 là :
\(\text{I2=U/R2}\)
\(\text{⇒R1/R2=I2/I1}\)
Mà : \(R_1=5R_2=>\dfrac{R_1}{R_2}=5\)
=> \(\dfrac{R_2}{R_1}=\dfrac{I_1}{I_2}=\dfrac{1}{5}\)
=>\(\text{I2=5I1 }\)(1)
Và : \(I_2=24-I_1\) (2)
Ta thay 5I1 ở (1) vào I2 ở (2) ta có :
\(5I_1=24-I_1\)
\(=>I_1=\dfrac{24}{5+1}=4\left(A\right)\)
\(I_2=24-I_1=24-4=20\left(A\right)\)
Điện trở R1 là :
\(R_1=\dfrac{U}{I_1}=\dfrac{U}{4}\left(\Omega\right)\)
Điện trở R2 là :
\(R_2=\dfrac{U}{I_2}=\dfrac{U}{20}\left(\Omega\right)\)
Thay giá trị HĐT U vào biểu thức rồi sẽ ra giá trị R1 và R2 nhé.

Tính điện trở R1 và R2 nheaa ??? Mình bổ sung :v
Ta có :
\(I=\dfrac{U}{R}\)
\(=>I_2=3I_1=>\dfrac{I_1}{I_2}=\dfrac{1}{3}\)
\(=>\dfrac{I_1}{I_2}=\dfrac{R_2}{R_1}=\dfrac{1}{3}\)
\(=>3R_2=R_1\) (1)
Theo đề : \(R_1=R_2+9\left(2\right)\)
Từ (1) và (2) có :
\(3R_2=R_2+9\)
\(=>R_2=\dfrac{9}{3-1}=4,5\left(\Omega\right)\)
\(=>R_1=R_2+9=13,5\Omega\)

Khi mắc nối tiếp cả 3 điện trở thì :R1 + R2 + R3 = U/I1=110/2=55. (1)
Khi mắc nối tiếp R1và R2 thì : R1 +R2 =U/I2=110/5,5=20. (2)
Khi mắc nối tiếp R1vaà R3 thì : R1 +R3=U/I3=110/2,2=50. (3)
Từ (1),(2) VÀ (3) ta có hệ pt : R1 + R2 + R3=55
R1 + R2 = 20
R1 + R3= 30
Giải ra,ta được :R1=15R2=5R3=35

Khi mắc nối tiếp cả 3 điện trở thì :R1 + R2 + R3 = U/I1=110/2=55. (1)
Khi mắc nối tiếp R1và R2 thì : R1 +R2 =U/I2=110/5,5=20. (2)
Khi mắc nối tiếp R1vaà R3 thì : R1 +R3=U/I3=110/2,2=50. (3)
Từ (1),(2) VÀ (3) ta có hệ pt : R1 + R2 + R3=55
R1 + R2 = 20
R1 + R3= 30
Giải ra,ta được :R1=15R2=5R3=35
Mắc nối tiếp cả 3 điện trở thì :
R1 +R2 +R3 =\(\frac{U}{I_1}\)=\(\frac{110}{2}\)=55 (1)
Mắc nối tiếp R1 và R2 thì :
R1 +R2 =\(\frac{U}{I_2}\)=\(\frac{110}{5,5}\)=20 (2)
Mắc nối tiếp R1 và R3 thì :
R1 +R3=\(\frac{U}{I_3}\)=\(\frac{110}{2,2}\)=50 (3)
Từ (1),(2) và (3) ta có hệ pt :
R1 +R2 +R3=55
R1 +R2=20
R1 +R3=50
Giải ra,ta sẽ có đáp án lần lượt là :R1=15
R2=5
R3=35
Tóm tắt :
\(R_1=5R_2\)
\(I_2=24-I_1\)
\(R_1//R_2\)
\(R_1=?R_2=?\)
GIẢI :
Ta có : R1//R2 nên :
\(U=U_1=U_2\)
Cường độ dòng điện qua điện trở R1 là :
\(I_1=\dfrac{U}{R_1}\)
Cường độ dòng điện qua điện trở R2 là :
\(I_2=\dfrac{U}{R_2}\)
\(\Rightarrow\dfrac{R_1}{R_2}=\dfrac{I_2}{I_1}\)
Mà : \(R_1=5R_2=>\dfrac{R_1}{R_2}=5\)
\(=>\dfrac{R_1}{R_2}=\dfrac{I_2}{I_1}=5\)
\(=>I_2=5I_1\) (1)
Và : \(I_2=24-I_1\) (2)
Ta thay 5I1 ở (1) vào I2 ở (2) ta có :
\(5I_1=24-I_1\)
\(\Rightarrow I_1=\dfrac{24}{6}=4\left(A\right)\)
\(I_2=24-I_1=24-4=20\left(A\right)\)
Điện trở R1 là :
\(I_1=\dfrac{U}{R_1}=>R_1=\dfrac{U}{I_1}=\dfrac{U}{4}\left(\Omega\right)\)
Điện trở R2 là :
\(I_2=\dfrac{U}{R_2}=>R_2=\dfrac{U}{I_2}=\dfrac{U}{20}\left(\Omega\right)\)
Thay giá trị HĐT U vào biểu thức rồi sẽ ra giá trị R1 và R2 nhé.