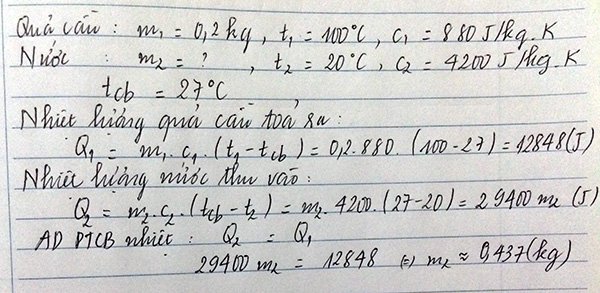Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham Khảo:
Do nước đá không tan hết nên khi cân bằng nhiệt thì hệ có nhiệt độ 0 độ C
Phương trình cân bằng nhiệt diễn tả quá trình cục nước đá tan một phần ba là:
M/3λ = m(c + c1).(10 - 0)
= m(c + c1).10 (1)
- Mặc dù nước đá mới tan có 1/3 nhưng thấy ngay là dù nước đá có tan hết thì mực nước trong cốc vẫn như vậy. Do đó lượng nước nóng đổ thêm vào để mực nước trong trạng thái cuối cùng tăng lên gấp đôi là: m + M.
Ta có phương trình cân bằng nhiệt:
2M/3λ + Mc(10 - 0) + m(c + c1)(10 - 0) = (M + m)c(40 -10)
=> 2M/3λ + 10Mc + 10m(c + c1)= 30(M + m)c
=> ((2/3)λ - 20c)M = m(2c - c1)10 (2)
Từ (1) và (2) ta có: λ/(2λ - 60c) = (c + c1)/(2c - c1)
=> 60c^2 = (3λ- 60c)c1
=> c1 = (20c^2)/(λ - 60c) = 1400J/kg.độ

Tham Khảo:
Do nước đá không tan hết nên khi cân bằng nhiệt thì hệ có nhiệt độ 0 độ C
Phương trình cân bằng nhiệt diễn tả quá trình cục nước đá tan một phần ba là:
M/3λ = m(c + c1).(10 - 0)
= m(c + c1).10 (1)
- Mặc dù nước đá mới tan có 1/3 nhưng thấy ngay là dù nước đá có tan hết thì mực nước trong cốc vẫn như vậy. Do đó lượng nước nóng đổ thêm vào để mực nước trong trạng thái cuối cùng tăng lên gấp đôi là: m + M.
Ta có phương trình cân bằng nhiệt:
2M/3λ + Mc(10 - 0) + m(c + c1)(10 - 0) = (M + m)c(40 -10)
=> 2M/3λ + 10Mc + 10m(c + c1)= 30(M + m)c
=> ((2/3)λ - 20c)M = m(2c - c1)10 (2)
Từ (1) và (2) ta có: λ/(2λ - 60c) = (c + c1)/(2c - c1)
=> 60c^2 = (3λ- 60c)c1
=> c1 = (20c^2)/(λ - 60c) = 1400J/kg.độ

a) Do trọng lượng riêng của nước đá là nhỏ hơn của nước nên đá nổi trên mặt trước khi đó một phần nước đá nhô lên khỏi mặt nước làm cho mực nước trong cố sẽ dâng lên khỏi miệng cốc và tổng thế tích là lớn hơn 500 cm3.
Trọng lượng của nước đá chính bằng trọng lượng phần nước bị nước đá chiếm chỗ (từ miệng cốc trở xuống )
=> Khi nước đá tan hết thì thể tích nước đá ban đầu đúng bằng thể tích phần nước bị nước đá chiếm chỗ, do đó mực nước trong cốc vẫn giữ nguyên như lúc đầu (đầy tới miệng cốc).
b) Tổng khối lượng của nước và nước đá chính bằng khối lượng của 500 cm3 nước và bằng 0,5 kg.
Gọi m (kg) là khối lượng của cục nước đá lúc đầu => Khối lượng của nước rót vào cốc là 0,5 - m (kg)
Phương trình cân bằng nhiệt: (0,5-m).4200.(35-15) = m\(\lambda\)+m.2100.(0-(-8))+4200.m.15
=> m = 0,084 kg=84g.

a) *Khi do m1 (kg) nước vào nhiệt lượng kế ,ta có pt :
Q0 = Q1
<=> m0.c1.(t0 - t1 ) = m1.c1 (t1 - tx)
<=>0,4 .(25-20 ) = m1 . (20 -tx )
<=> m1 (20 - tx ) = 2
<=> tx = \(\dfrac{20m_1-2}{m_1}\) (1)
*Khi bỏ cục đá vào nhiệt lượng kế :
Ta co : M = m0 + m1 + m2
=> m2 = M- m0 - m1 = 0,7 - 0,4 - m1 = 0,3 - m1
Nhiệt lượng tổng cộng của cục đá :
Qda = Q-10 den 0 + Q0*C + Q0 den t3
<=> Qda = m2.c2. (0 - t2 ) + m2 .\(\curlywedge\) + m2 . c1 ( t3 - 0)
<=> Qda = (0,3 - m1 ) .2100.10+ (0,3 - m1 ).336000 + (0,3 - m1 ) 4200.5
<=> Qda = 378 000 (0,3 - m1 )
<=> Qda = 113400 - 378000m1
Nhiệt lượng tỏa ra của nước trong nhiệt lượng kế :
Qnuoc = (0,4+m1). c1.(t1- t3)= (0,4+ m1).4200.(20-5)= 25 200+63000m1
Áp dụng pt cân bằng nhiệt , ta có :
Qda = Qnuoc
<=> 113 400 - 378 000 m1 = 25 200 + 63 000 m1
<=> m1 = 0,2
=> m2 = 0,3 - m1 = 0,3 - 0,2 = 0,1
Vay......................
b) Thay m1 = 0,2 vào (1) , tá dược :
tx = \(\dfrac{20m_1-2}{m_1}=\dfrac{20.0,2-2}{0,2}=10\)
Vay ....................

Đáp án: B
- Nhiệt lượng do cốc và nước toả ra để hạ nhiệt độ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của khối nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Vì Q 1 > Q 2 nên khối nước đá đã tan hết và nhiệt độ hỗn hợp lớn hơn 0 0 C

Gọi khối lượng nước rót sang là m ; nhiệt độ cân bằng lần 1 là t3 , lần 2 là t4 (0 < m < 4 ; t4 > t3)
Rót m lượng nước từ 1 sang 2 => lượng nước m tỏa nhiệt hạ từ 68oC đến t3oC ; 5 kg nước bình 2 thu nhiệt tăng
từ 20oC lên toC
Phương trình cân bằng nhiệt :
m.c.(68-t3) = 5.c.(t3 - 20)
=> m.(68-t3) = 5.(t3 - 20)
=> 68m - mt3 = 5t3 - 100 (1)
Rót m lượng nước từ bình 2 sang bình 1 sau khi cân bằng nhệt, lượng nước m thu nhiệt tăng từ t3 oC lên t4 oC ; lượng nước
còn lại trong bình 1 tỏa nhiệt hạ từ 68oC xuống t4oC
Phương trình cân bằng nhiệt
m.c.(t4 - t3) = (4 - m).c(68 - t4)
=> m.(t4 - t3) = (4 - m)(68 - t4)
=> -mt3 = 272 - 4t4 - 68m
=> 68m - mt3 = 272 - 4t4 (2)
Từ (1)(2) => 272 - 4t4 = 5t3 - 100
<=> 372 - 4(t4 - t3) = 9t3
<=> t3 > 34,2 (Vì t4 - t3 < 16)
Khi đó 5(t3 - 20) > 71
=> m(68 - t3) > 71
=> m > 2,1
Vậy 2,1 < m < 4