Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi quãng đường từ xã KN tới KA là x (x > 0)
Thời gian lúc đi là : x/15 (h)
Thời gian lúc về là: x/12 (h)
Thời gian lúc về nhiều hơn lúc đi là: 45' = 3/4 (h)
Ta có phương trình: \(\dfrac{x}{12}-\dfrac{x}{15}=\dfrac{3}{4}\Leftrightarrow5x-4x=45\Leftrightarrow x=45\left(km\right)\)
Vậy quãng đường từ xã KN đến KA dài 45km.
Gọi:
Độ dài quãng đường từ Kỳ Ninh tới Kỳ Anh là: S (km) với S nguyên dương.
Thời gian lúc đi là: \(\dfrac{S}{15}\) (h).
Thời gian lúc về là: \(\dfrac{S}{12}\) (h).
Theo đề bài, ta có:
\(\dfrac{S}{12}\) - \(\dfrac{S}{15}\)= \(\dfrac{45}{60}\)=\(\dfrac{3}{4}\)
=> \(\dfrac{S}{60}\)=\(\dfrac{3}{4}\)
=> S= \(\dfrac{3.60}{4}\)=45
vậy độ dài quãng đường từ Kỳ Ninh đến Kỳ Anh là 45 km.

Câu 2:
a: Không
b: Không
Câu 3:
a: \(\widehat{B}=\widehat{zAB}\left(=124^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên Bt//Az
b: n\(\perp\)DC
m\(\perp\)DC
Do đó: n//m
c: \(\widehat{xEG}+\widehat{yGE}=70^0+110^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Ex//Gy
d: Vẽ lại hình, ta sẽ có:
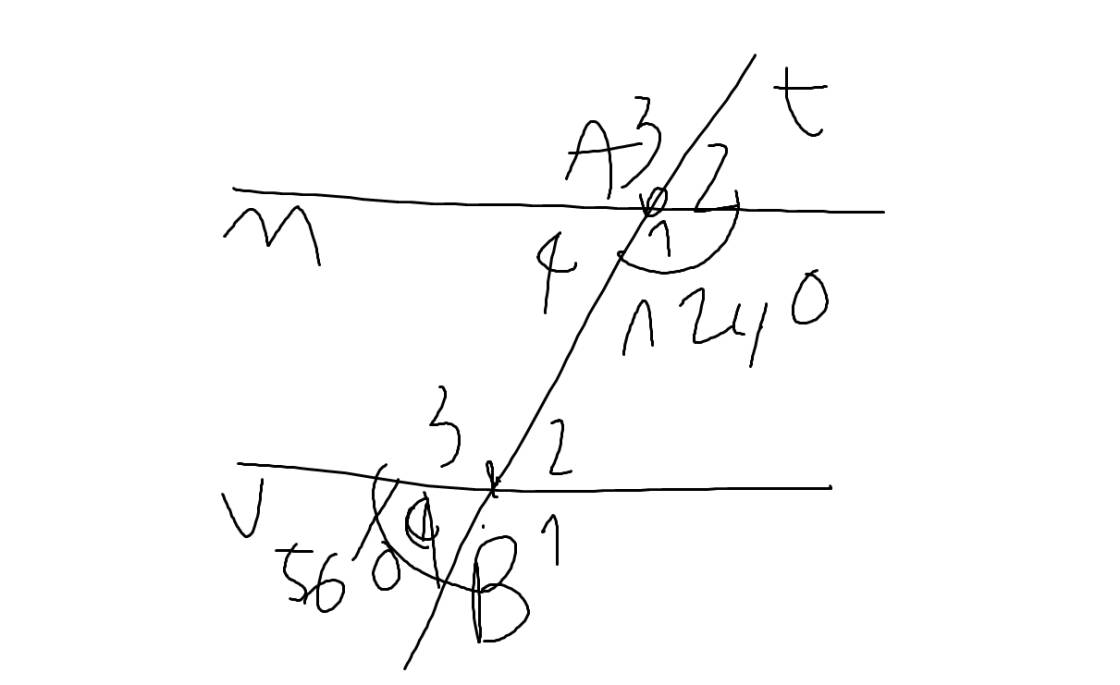
Ta có: \(\widehat{B_4}=\widehat{B_2}\)(hai góc đối đỉnh)
mà \(\widehat{B_4}=56^0\)
nên \(\widehat{B_2}=56^0\)
Ta có: \(\widehat{A_1}+\widehat{B_2}=124^0+56^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên m//v

Ta có MD // AE (vì MD // AB)
ME //AD (vì ME // AC)
Nên AEMD là hình bình hành, I là trung điểm của DE nên I cũng là trung điểm của AM, do đó A đối xứng với M qua I
GT: Cho hình 82, trong đó MD // AB, ME // AC
KL: Chứng minh A đối xứng với M qua I
GIẢI:
Ta có: MD // AE (vì MD // AB)
ME // AD (vì ME // AC)
Nên AEMD là hình bình hành, I là trung điểm của DE nên I cũng là trung điểm của AM, do đó A đối xứng với M qua I

a: MNPQ là hình bình hành
=>MQ//NP
=>MQ//IP
Xét tứ giác MIPQ có IP//MQ
nên MIPQ là hình thang
b: ΔMNP vuông cân tại N
=>MN=NP và \(\widehat{MNP}=90^0\)
Hình bình hành MNPQ có \(\widehat{MNP}=90^0\)
nên MNPQ là hình chữ nhật
=>\(\widehat{Q}=\widehat{P}=90^0\)
Xét ΔMNI vuông tại N có \(sinNMI=\dfrac{NI}{MN}=\dfrac{2}{3}\)
nên \(\widehat{NMI}\simeq42^0\)
\(\widehat{NMI}+\widehat{QMI}=\widehat{NMQ}=90^0\)
=>\(\widehat{QMI}+42^0=90^0\)
=>\(\widehat{QMI}=48^0\)
IP//MQ
=>\(\widehat{QMI}+\widehat{MIP}=180^0\)(hai góc trong cùng phía)
=>\(\widehat{MIP}+48^0=180^0\)
=>\(\widehat{MIP}=132^0\)
 may bai nay kho qua giup em , em dang can gap a
may bai nay kho qua giup em , em dang can gap a
tớ không biết dài quá
2,052641236x10^20