Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Đường thẳng d đi qua M1( -3 ; -2 ; 6) và có vectơ chỉ phương (2 ; 3 ; 4).
Đường thẳng d' đi qua M2( 5 ; -1 ; 20) và có vectơ chỉ phương (1 ; -4 ; 1).
Ta có = (19 ; 2 ; -11) ;
= (8 ; 1 ; 14)
và = (19.8 + 2 - 11.4) = 0
nên d và d' cắt nhau.
Nhận xét : Ta nhận thấy ,
không cùng phương nên d và d' chỉ có thể cắt nhau hoặc chéo nhau.
Xét hệ phương trình:
Từ (1) với (3), trừ vế với vế ta có 2t = 6 => t = -3, thay vào (1) có t' = -2, từ đó d và d' có điểm chung duy nhất M(3 ; 7 ; 18). Do đó d và d' cắt nhau.
b) Ta có : (1 ; 1 ; -1) là vectơ chỉ phương của d và
(2 ; 2 ; -2) là vectơ chỉ phương của d' .
Ta thấy và
cùng phương nên d và d' chỉ có thể song song hoặc trùng nhau.
Lấy điểm M(1 ; 2 ; 3) ∈ d ta thấy M d' nên d và d' song song.
Xét hệ
Hai đường thẳng d và d' cắt nhau khi và chỉ khi hệ có nghiệm duy nhất.
Nhân hai về của phương trình (3) với 2 rồi cộng vế với vế vào phương trình (2), ta có t = 2;
s = 0. Thay vào phương trình (1) ta có 1 + 2a = 1 => a =0.
Vậy a = 0 thì d và d' cắt nhau.
Xét hệ
Hai đường thẳng d và d' cắt nhau khi và chỉ khi hệ có nghiệm duy nhất.
Nhân hai về của phương trình (3) với 2 rồi cộng vế với vế vào phương trình (2), ta có t = 2;
s = 0. Thay vào phương trình (1) ta có 1 + 2a = 1 => a =0.
Vậy a = 0 thì d và d' cắt nhau.
a) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
3(12 + 4t) +5(9 + 3t) - (1 + t) = 0
⇔ 26t + 78 = 0 ⇔ t = -3.
Tức là d ∩ (α) = M(0 ; 0 ; -2).
Trong trường hợp này d cắt (α) tại điểm M.
b) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + t) + 3.(2 - t) + (1 + 2t) + 1 = 0
⇔ 0.t + t = 9, phương trình vô nghiệm.
Chứng tỏ d và (α) không cắt nhau., ta có d // (α).
c) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + 1) + (1+ 2t) + (2 - 3t) - 4 = 0
⇔ 0t + 0 = 0,phương trình này có vô số nghiệm, chứng tỏ d ⊂ (α) .
a) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
3(12 + 4t) +5(9 + 3t) - (1 + t) = 0
⇔ 26t + 78 = 0 ⇔ t = -3.
Tức là d ∩ (α) = M(0 ; 0 ; -2).
Trong trường hợp này d cắt (α) tại điểm M.
b) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + t) + 3.(2 - t) + (1 + 2t) + 1 = 0
⇔ 0.t + t = 9, phương trình vô nghiệm.
Chứng tỏ d và (α) không cắt nhau., ta có d // (α).
c) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + 1) + (1+ 2t) + (2 - 3t) - 4 = 0
⇔ 0t + 0 = 0,phương trình này có vô số nghiệm, chứng tỏ d ⊂ (α) .
Đường thẳng d qua điểm M(1 ; 2 ; 0) và có vec tơ chỉ phương (-1 ; 2 ; 3).
Đường thẳng d' qua điểm M'(1 ; 3 ;1) và có vectơ chỉ phương (1 ; -2 ; 0).
Cách 1. Xét
= (2 ; 1 ;-5).
= (0 ; 1 ; 1).
Ta có : = 2.0 + 1.1 + (-5).1 = -4 ≠ 0.
Do đó d và d' chéo nhau.
Cách 2: Vì và
không cùng phương nên d và d' chỉ có thể là chéo nhau hoặc cắt nhau.
Ta xét giao điểm của d và d':
=>
hệ vô nghiệm.
Do đó d và d' không thể cắt nhau. Vì vậy d và d' chéo nhau.
Đường thẳng ∆ qua điểm M(-3 ; -1 ; -1) có vectơ chỉ phương (2 ; 3 ; 2).
Mặt phẳng (α) có vectơ pháp tuyến (2 ; -2 ; 1).
Ta có M (α) và
= 0 nên ∆ // (α).
Do vậy d(∆,(α)) = d(M,(α)) = .
Đường thẳng ∆ qua điểm M(-3 ; -1 ; -1) có vectơ chỉ phương (2 ; 3 ; 2).
Mặt phẳng (α) có vectơ pháp tuyến (2 ; -2 ; 1).
Ta có M (α) và
= 0 nên ∆ // (α).
Do vậy d(∆,(α)) = d(M,(α)) =
a) Xét mặt phẳng (P) đi qua d và (P) ⊥ (Oxy), khi đó ∆ = (P) ∩ (Oxy) chính là hình chiếu vuông góc của d lên mặt phẳng (Oxy).
Phương trình mặt phẳng (Oxy) có dạng: z = 0 ; vectơ (0 ; 0 ;1) là vectơ pháp tuyến của (Oxy), khi đó
và
( 1 ; 2 ; 3) là cặp vectơ chỉ phương của mặt phẳng (P).
= (2 ; -1 ; 0) là vectơ pháp tuyến của (P).
Phương trình mặt phẳng (P) có dạng:
2(x - 2) - (y + 3) +0.(z - 1) = 0
hay 2x - y - 7 = 0.
Đường thẳng hình chiếu ∆ thỏa mãn hệ:
Điểm M0( 4 ; 1 ; 0) ∈ ∆ ; vectơ chỉ phương của ∆ vuông góc với
và vuông góc với
, vậy có thể lấy
= (1 ; 2 ; 0).
Phương trình tham số của hình chiếu ∆ có dạng:
.
Chú ý :
Ta có thể giải bài toán này bằng cách sau:
Lấy hai điểm trên d và tìm hình chiếu vuông góc của nó trên mặt phẳng (Oxy). Đường thẳng đi qua hai điểm đó chính là hình chiếu cần tìm.
Chẳng hạn lấy M1( 2 ; 3 ; -1) ∈ d và M2( 0 ; -7 ; -5) ∈ d, hình chiếu vuông góc của
M1 trên (Oxy) là N1 (2 ; -3 ; 0), hình chiếu vuông góc của M2 trên (Oxy) là N2(0 ; -7 ; 0).
Đườn thẳng ∆ qua N1, N2 chính là hình chiếu vuông góc của d lên (Oxy).
Ta có : (-2 ; -4 ; 0) //
(1 ; 2 ; 0).
Phương trình tham số của ∆ có dạng:
.
b) Tương tự phần a), mặt phẳng (Oxy) có phương trình x = 0.
lấy M1( 2 ; 3 ; -1) ∈ d và M2( 0 ; -7 ; -5) ∈ d, hình chiếu vuông góc của
M1 trên (Oxy) là M'1 (0 ; -3 ; 1), hình chiếu vuông góc của M2 trên (Oyz) là chính nó.
Đườn thẳng ∆ qua M'1, M2 chính là hình chiếu vuông góc của d lên (Oyz).
Ta có: (0 ; -4 ; -6) //
(0 ; 2 ; 3).
Phương trình M'1M2 có dạng:
.
a) Đường thẳng d đi qua M1( -3 ; -2 ; 6) và có vectơ chỉ phương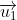
(2 ; 3 ; 4).
Đường thẳng d' đi qua M2( 5 ; -1 ; 20) và có vectơ chỉ phương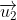
(1 ; -4 ; 1).
Ta có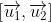
= (19 ; 2 ; -11) ; 
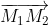= (8 ; 1 ; 14)
và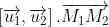
= (19.8 + 2 - 11.4) = 0
nên d và d' cắt nhau.
Nhận xét : Ta nhận thấy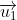
, 
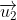không cùng phương nên d và d' chỉ có thể cắt nhau hoặc chéo nhau.
Xét hệ phương trình: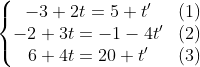
Từ (1) với (3), trừ vế với vế ta có 2t = 6 => t = -3, thay vào (1) có t' = -2, từ đó d và d' có điểm chung duy nhất M(3 ; 7 ; 18). Do đó d và d' cắt nhau.
b) Ta có :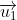
(1 ; 1 ; -1) là vectơ chỉ phương của d và 
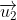(2 ; 2 ; -2) là vectơ chỉ phương của d' .
Ta thấy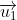
và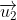 
cùng phương nên d và d' chỉ có thể song song hoặc trùng nhau.
Lấy điểm M(1 ; 2 ; 3) ∈ d ta thấy M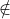
d' nên d và d' song song.