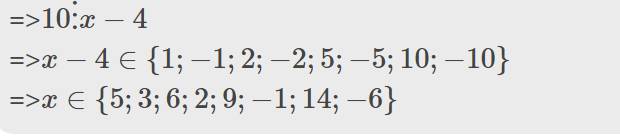Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(P=x^4+2x^2+1-x^2=\left(x^2+1\right)^2-x^2\)
\(P=\left(x^2-x+1\right)\left(x^2+x+1\right)\)
\(\Rightarrow\) P luôn có ít nhất 2 ước số là \(x^2-x+1\) và \(x^2+x+1\)
Do \(x^2+x+1\ge x^2-x+1\) nên P là SNT khi và chỉ khi \(x^2-x+1=1\) đồng thời \(x^2+x+1\) là SNT
\(x^2-x+1=1\Leftrightarrow x^2-x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
- Với \(x=0\Rightarrow x^2+x+1=1\) ko phải SNT (loại)
- Với \(x=1\Rightarrow x^2+x+1=3\) là SNT (t/m)
Vậy \(x=1\)

1: \(D=\dfrac{1}{x+4}+\dfrac{x}{x-4}+\dfrac{24-x^2}{x^2-16}\)
\(=\dfrac{1}{x+4}+\dfrac{x}{x-4}+\dfrac{24-x^2}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{x-4+x\left(x+4\right)+24-x^2}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{-x^2+x+20+x^2+4x}{\left(x+4\right)\left(x-4\right)}=\dfrac{5x+20}{\left(x+4\right)\left(x-4\right)}\)
\(=\dfrac{5\left(x+4\right)}{\left(x+4\right)\left(x-4\right)}=\dfrac{5}{x-4}\)
2: Khi x=10 thì \(D=\dfrac{5}{10-4}=\dfrac{5}{6}\)
3: \(M=\left(x-2\right)\cdot D=\dfrac{5\left(x-2\right)}{x-4}\)
Để M là số nguyên thì \(5\cdot\left(x-2\right)⋮x-4\)
=>\(5\left(x-4+2\right)⋮x-4\)
=>\(5\left(x-4\right)+10⋮x-4\)
=>\(10⋮x-4\)
=>\(x-4\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
=>\(x\in\left\{5;3;6;2;9;-1;14;-6\right\}\)


\(B=\left(n+3\right)^2-\left(n-4\right)^2\)
\(=\left(n+3-n+4\right)\left(n+3+n-4\right)\)
\(=7\left(2n-1\right)\)
Dễ thấy B là số nguyên tố khi
\(2n-1=1\Leftrightarrow n=1\)
Vậy n = 1 thì B là số nguyên tố